早教吧作业答案频道 -->数学-->
已知函数.(I)当-1<a<0时,求f(x)的单调区间;(II)若-1<a<2(ln2-1),求证:函数f(x)只有一个零点x,且a+1<x<a+2;(III)当时,记函数f(x)的零点为x,若对任意x
题目详情
已知函数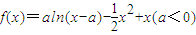 .
.
(I)当-1<a<0时,求f(x)的单调区间;
(II)若-1<a<2(ln2-1),求证:函数f(x)只有一个零点x ,且a+1<x <a+2;
(III)当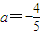 时,记函数f(x)的零点为x ,若对任意x 1 ,x 2 ∈[0,x ]且x 2 -x 1 =1,都有|f(x 2 )-f(x 1 )|≥m成立,求实数m的最大值.
时,记函数f(x)的零点为x ,若对任意x 1 ,x 2 ∈[0,x ]且x 2 -x 1 =1,都有|f(x 2 )-f(x 1 )|≥m成立,求实数m的最大值.
(本题可参考数据:ln2=0.7,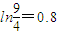 ,
,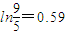 )
)
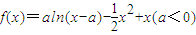 .
.(I)当-1<a<0时,求f(x)的单调区间;
(II)若-1<a<2(ln2-1),求证:函数f(x)只有一个零点x ,且a+1<x <a+2;
(III)当
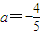 时,记函数f(x)的零点为x ,若对任意x 1 ,x 2 ∈[0,x ]且x 2 -x 1 =1,都有|f(x 2 )-f(x 1 )|≥m成立,求实数m的最大值.
时,记函数f(x)的零点为x ,若对任意x 1 ,x 2 ∈[0,x ]且x 2 -x 1 =1,都有|f(x 2 )-f(x 1 )|≥m成立,求实数m的最大值.(本题可参考数据:ln2=0.7,
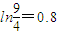 ,
,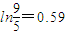 )
)▼优质解答
答案和解析
分析:
(I)f(x)的定义域为(a,+∞)..由此能求出题函数f(x)的单调区间.(II)当-1<a<2(ln2-1)<0时,由(I)知,f(x)的极小值为f(0),极大值为f(a+1).由此能够证明函数f(x)只有一个零点x,且a+1<x<a+2.(III)因为,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.由此能推导出使得|f(x2)-f(x1)|≥m恒成立的m的最大值.
(I)f(x)的定义域为(a,+∞)..令f'(x)=0?x=0或x=a+1.当-1<a<0时,a+1>0,函数f(x)与f'(x)随x的变化情况如下表:x(a,0)(0,a+1)a+1(a+1,+∞)f(x)-+-f'(x)↘极小值↗极大值↘所以,函数f(x)的单调递增区间是(0,a+1),单调递减区间是(a,0)和(a+1,+∞).…(4分)(II)证明:当-1<a<2(ln2-1)<0时,由(I)知,f(x)的极小值为f(0),极大值为f(a+1).因为f(0)=aln(-a)>0,,且f(x)在(a+1,+∞)上是减函数,所以f(x)至多有一个零点.又因为,所以函数f(x)只有一个零点x,且a+1<x<a+2.…(9分)(III)因为,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.因为函数f(x)在[0,a+1]上是增函数,在(a+1,+∞)上是减函数,所以f(x1)≥f(0),f(x2)≤f(1),∴f(x1)-f(x2)≥f(0)-f(1).当时,.所以f(x1)-f(x2)≥f(0)-f(1)>0所以|f(x2)-f(x1)|的最小值为.所以使得|f(x2)-f(x1)|≥m恒成立的m的最大值为.…(14分)
点评:
本题考查函数的单调区间的求法,考查不等式的证明,考查满足条件的实数的最大值的求法,考查推理论证能力,考查等价转化思想,解题时要认真审题,注意导数性质的合理运用.
分析:
(I)f(x)的定义域为(a,+∞)..由此能求出题函数f(x)的单调区间.(II)当-1<a<2(ln2-1)<0时,由(I)知,f(x)的极小值为f(0),极大值为f(a+1).由此能够证明函数f(x)只有一个零点x,且a+1<x<a+2.(III)因为,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.由此能推导出使得|f(x2)-f(x1)|≥m恒成立的m的最大值.
(I)f(x)的定义域为(a,+∞)..令f'(x)=0?x=0或x=a+1.当-1<a<0时,a+1>0,函数f(x)与f'(x)随x的变化情况如下表:x(a,0)(0,a+1)a+1(a+1,+∞)f(x)-+-f'(x)↘极小值↗极大值↘所以,函数f(x)的单调递增区间是(0,a+1),单调递减区间是(a,0)和(a+1,+∞).…(4分)(II)证明:当-1<a<2(ln2-1)<0时,由(I)知,f(x)的极小值为f(0),极大值为f(a+1).因为f(0)=aln(-a)>0,,且f(x)在(a+1,+∞)上是减函数,所以f(x)至多有一个零点.又因为,所以函数f(x)只有一个零点x,且a+1<x<a+2.…(9分)(III)因为,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.因为函数f(x)在[0,a+1]上是增函数,在(a+1,+∞)上是减函数,所以f(x1)≥f(0),f(x2)≤f(1),∴f(x1)-f(x2)≥f(0)-f(1).当时,.所以f(x1)-f(x2)≥f(0)-f(1)>0所以|f(x2)-f(x1)|的最小值为.所以使得|f(x2)-f(x1)|≥m恒成立的m的最大值为.…(14分)
点评:
本题考查函数的单调区间的求法,考查不等式的证明,考查满足条件的实数的最大值的求法,考查推理论证能力,考查等价转化思想,解题时要认真审题,注意导数性质的合理运用.
看了 已知函数.(I)当-1<a<...的网友还看了以下:
定义在R上的函数f(x)满足f(x+1)=2f(x).若当0≤x≤1时.f(x)=x(1-x),则 2020-04-06 …
设函数f(x)=1/2x2ex求f(x)的单调区间还有若当-2≤x≤2时,f(x)>m恒成立,求m 2020-06-08 …
设y=f(x)是R上的奇函数,且当x∈R是,都有f(x+2)=-f(x)若当-1≤x≤1时,f(x 2020-06-09 …
设函数f(x)=(1-mx)ln(1+x).(1)若当0<x<1时,函数f(x)的图象恒在直线y= 2020-07-19 …
设y=f(x)是R上的奇函数,且当x∈R是,都有f(x+2)=-f(x)(1)试证明f(x)是周期 2020-08-01 …
已知f(x)是定义在R上的偶函数,且f(x+4)=f(x)(x∈R)若当0≤x≤2时f(x)=x求 2020-08-01 …
铜陵三中文科生求填空题解题过程:)定义在R上的偶函数f(x)满足f(x+2)-f(x)=2f(1). 2020-11-12 …
若定义[a]表示不大于实数a的最大整数(例如当-2≤a<-1时,[a]=-2;0≤a<1时,[a]= 2020-12-08 …
定义在R上的函数f(X)满足f(X+1)=2f(X),若当0≤x≤1时,f(X)=x(1-x),则当 2020-12-27 …
知一次函数y=kx+b的图像经过A(2,1),(1)若这条直线和x轴成45°角,((2)若当-1≤x 2021-02-04 …