早教吧作业答案频道 -->数学-->
如图,圆柱O-O1中,AB为下底面圆O的直径,CD为上底面圆O1的直径,AB∥CD,点E、F在圆O上,且AB∥EF,且AB=2,AD=1.(Ⅰ)求证:平面ADF⊥平面CBF;(Ⅱ)若DF与底面所成角为π4,求几何体EF-ABC
题目详情
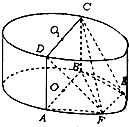
如图,圆柱O-O1中,AB为下底面圆O的直径,CD为上底面圆O1的直径,AB∥CD,点 E、F在圆O上,且AB∥EF,且AB=2,AD=1.
(Ⅰ)求证:平面ADF⊥平面CBF;
(Ⅱ)若DF与底面所成角为
,求几何体EF-ABCD的体积.

(Ⅰ)求证:平面ADF⊥平面CBF;
(Ⅱ)若DF与底面所成角为
| π |
| 4 |
▼优质解答
答案和解析
 (Ⅰ)证明:由已知,AF⊥BF,AD⊥BF,且AF∩AD=A,故BF⊥平面ADF,
(Ⅰ)证明:由已知,AF⊥BF,AD⊥BF,且AF∩AD=A,故BF⊥平面ADF,
所以平面ADF⊥平面CBF.…(5分)
(Ⅱ) 因AD垂直于底面,若DF与底面所成角为
,则∠AFD=
,故AF=1,
则四棱锥F-ABCD的高为
,又SABCD=2,VF-ABCD=
×
×2=
;
三棱锥C-BEF的高为1,而△BEF中,BE=BF=1,∠BEF=120°,
所以SBEF=
,则VC-BEF=
×1×
=
,
所以几何体EF-ABCD的体积为
.…(12分)
 (Ⅰ)证明:由已知,AF⊥BF,AD⊥BF,且AF∩AD=A,故BF⊥平面ADF,
(Ⅰ)证明:由已知,AF⊥BF,AD⊥BF,且AF∩AD=A,故BF⊥平面ADF,所以平面ADF⊥平面CBF.…(5分)
(Ⅱ) 因AD垂直于底面,若DF与底面所成角为
| π |
| 4 |
| π |
| 4 |
则四棱锥F-ABCD的高为
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
三棱锥C-BEF的高为1,而△BEF中,BE=BF=1,∠BEF=120°,
所以SBEF=
| ||
| 4 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
所以几何体EF-ABCD的体积为
5
| ||
| 12 |
看了 如图,圆柱O-O1中,AB为...的网友还看了以下:
会做的来解决看,看看你有多厉害、、、、已知定义域为R的函数f(x)在8到正无穷上是减函数,且函数y 2020-04-26 …
,;定义在正整数集f(x)对任意m,n,都有f(m+n)=f(m)+f(n)+4(m+n)-2,且 2020-05-13 …
周期函数问题f(x)=-f(x+1)=f((x+1)+1)=f(x+2)“f(x)=-f(x+1) 2020-05-14 …
f(x)是定义在R上的函数,且对任意实数x,y都有f(x+y)=f(x)+f(y)-1成立,当f( 2020-06-02 …
设在区间[0,1]上f''(x)>0,则f'(0)f'(1)和f(1)-f(0)的大小顺序是设在区 2020-06-08 …
已知集合M={f(x)|f(-x)=f(x),x∈R};N={f(x)|f(-x)=-f(x),x 2020-07-30 …
若函数f(x)不等于0,且f(x)满足下列三个条件:1.对任意实数a、b,均有f(a-b)=f(a 2020-08-03 …
已知f(x)在R上是增函已知f(x)在R上是增函数,a,b∈R,且a+b≤0,则有[]A、f(a)+ 2020-12-08 …
如图所示,用一根不可伸长的轻质细线将小球悬挂在天花板上,现对小球施加一个方向始终垂直细线的拉力F将小 2020-12-24 …
f(x+y)=f(x)*f(y)f(x+y)=f(x)·f(y),且f(1)=2求f(2)/f(1) 2020-12-26 …