早教吧作业答案频道 -->数学-->
设连接双曲线与的4个顶点的四边形面积为S1,连接其4个焦点的四边形面积为S2,则的最大值为.
题目详情
设连接双曲线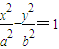 与
与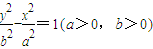 的4个顶点的四边形面积为S 1 ,连接其4个焦点的四边形面积为S 2 ,则
的4个顶点的四边形面积为S 1 ,连接其4个焦点的四边形面积为S 2 ,则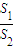 的最大值为 .
的最大值为 .
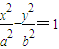 与
与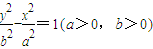 的4个顶点的四边形面积为S 1 ,连接其4个焦点的四边形面积为S 2 ,则
的4个顶点的四边形面积为S 1 ,连接其4个焦点的四边形面积为S 2 ,则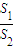 的最大值为 .
的最大值为 .▼优质解答
答案和解析
分析:
根据对称性,两个四边形的面积都可以分为四个全等的直角三角形的面积,两个面积的比值用a,b表示出来,再根据基本不等式求最大值.
设双曲线的右顶点为A,其坐标是(a,0),由焦点为C,坐标为;设双曲线上顶点为B,坐标为(0,b),上焦点为D,坐标为.O为坐标原点.则S1=4S△OAB=2ab,S2=4S△OCD=2(a2+b2),所以.故答案为.
点评:
本题考查双曲线的简单几何性质和使用基本不等式求二元函数的最值.
考点:
圆锥曲线与方程、不等式.
分析:
根据对称性,两个四边形的面积都可以分为四个全等的直角三角形的面积,两个面积的比值用a,b表示出来,再根据基本不等式求最大值.
设双曲线的右顶点为A,其坐标是(a,0),由焦点为C,坐标为;设双曲线上顶点为B,坐标为(0,b),上焦点为D,坐标为.O为坐标原点.则S1=4S△OAB=2ab,S2=4S△OCD=2(a2+b2),所以.故答案为.
点评:
本题考查双曲线的简单几何性质和使用基本不等式求二元函数的最值.
考点:
圆锥曲线与方程、不等式.
看了设连接双曲线与的4个顶点的四边...的网友还看了以下:
已知二次函数y=x*x+4x与x轴交于B,O两点,顶点为A,连接AB,过原点O作AB的平行线得到直 2020-04-27 …
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在 2020-05-13 …
平面直角坐标系中,正方形ABCD四个顶点的坐标分别为(-1,-1)(1,-1)(1,1)(-1,1 2020-05-16 …
如图1,正方形ABCD是边长为1的正方形,正方形EFGH的边HE、HG与正方形ABCD的边AB、B 2020-06-12 …
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在 2020-06-14 …
欧拉公式变形公式探究(类似于找规律)月考试题:一个多面体由三角形和正八边形组成V(顶点数)+F(面 2020-06-27 …
已知P为椭圆上一点已知P为椭圆x^2/a^2+y^2/b^2=1(a>b>0)上一点,F1,F2为 2020-06-30 …
假设三角形有两个顶点在正方形同一条边m上,则另外一个顶点在m邻边或者对边上,这两种情况下三角形逗不 2020-07-12 …
如图,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的4条边的小 2020-11-04 …
设△三边上的三个内接正方形(两个顶点在三角形的一边上,其余两个顶点分别在三角形的另两边上)的面积相等 2021-02-04 …