定义:如果一个与的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是与的“反比例平移函数”.例如:的图象向左平移2
定义:如果一个 ![]() 与
与 ![]() 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是
的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是 ![]() 与
与 ![]() 的“反比例平移函数”.
的“反比例平移函数”.
例如 : ![]() 的图象向左平移 2 个单位,再向下平移 1 个单位得到
的图象向左平移 2 个单位,再向下平移 1 个单位得到 ![]() 的图象,则
的图象,则 ![]() 是
是 ![]() 与
与 ![]() 的“反比例平移函数”.
的“反比例平移函数”.
( 1 ) 若矩形的两边分别是 2 ![]() 、 3
、 3 ![]() ,当这两边分别增加
,当这两边分别增加 ![]() (
( ![]() ) 、
) 、 ![]() (
( ![]() ) 后,得到的新矩形的面积为 8
) 后,得到的新矩形的面积为 8 ![]() ,求
,求 ![]() 与
与 ![]() 的函数表达式,并判断这个函数是否为“反比例平移函数”.
的函数表达式,并判断这个函数是否为“反比例平移函数”.
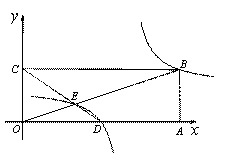
( 2 )如图,在平面直角坐标系中,点 ![]() 为原点,矩形
为原点,矩形 ![]() 的顶点
的顶点 ![]() 、
、 ![]() 的坐标分别为 (9 , 0) 、 (0 , 3) .点
的坐标分别为 (9 , 0) 、 (0 , 3) .点 ![]() 是
是 ![]() 的中点,连接
的中点,连接 ![]() 、
、 ![]() 交于点
交于点 ![]() ,“反比例平移函数”
,“反比例平移函数” ![]() 的图象经过
的图象经过 ![]() 、
、 ![]() 两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
( ![]() 3 )在( 2 )的条件下, 已知过线段
3 )在( 2 )的条件下, 已知过线段 ![]() 中点的一条直线
中点的一条直线 ![]() 交这个“反
交这个“反
比例平移函数”图象于 ![]() 、
、 ![]() 两点 (
两点 ( ![]() 在
在 ![]() 的右侧 ) , 若
的右侧 ) , 若 ![]() 、
、 ![]() 、
、
![]() 、
、 ![]() 为顶点组成的四边形面积为 16 ,请求出点
为顶点组成的四边形面积为 16 ,请求出点 ![]() 的坐标.
的坐标.
( 1 ) ![]() ,
,
∴ ![]()
![]() 向右平移 2 个单位,再向上平移 3 个单位得到
向右平移 2 个单位,再向上平移 3 个单位得到 ![]() . ∴
. ∴ ![]() 是 “反比例平移函数” . ……2 分
是 “反比例平移函数” . ……2 分
( 2 ) “反比例平移函数”的表达式为 ![]() .
.
变换后的反比例函数表达式为 ![]() .
.
( 3 ) 如图, 当点 ![]() 在点
在点 ![]() 左侧时, 设线段
左侧时, 设线段 ![]() 的中点为
的中点为 ![]() ,由反比
,由反比
例函数中心对称性,四边形 ![]() 为平行四边形 .
为平行四边形 .
∵四边形 ![]() 的面积为 16 ,∴
的面积为 16 ,∴ ![]() =4 ,
=4 ,
∵ ![]() (9 3) ,
(9 3) , ![]() (6 2).
(6 2).
![]() 是
是 ![]() 的 “反比例平移函数”,
的 “反比例平移函数”,
∴ ![]() =
= ![]() =4 ,
=4 , ![]()
![]() (3 1)
(3 1)
过 ![]() 作
作 ![]() 轴的垂线,与
轴的垂线,与 ![]() 、
、 ![]() 轴分别交于
轴分别交于 ![]() 、
、 ![]() 点 .
点 .
![]() .
.
设 ![]() ,
,
∴ 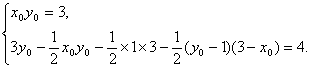
即 
∴ 
∴ ![]() (1 , 3) , ∴点
(1 , 3) , ∴点 ![]() 的坐标为( 7 , 5 ) .
的坐标为( 7 , 5 ) .
当点 ![]() 在点
在点 ![]() 右侧时, 同理可得 点
右侧时, 同理可得 点 ![]() 的坐标为( 15 ,
的坐标为( 15 , ![]() ) .
) .

![]()
怎样判断化合反应?木炭+氧气——二氧化碳是不是化合反应?氢气+氧气——水是不是化合反应?怎么判断某 2020-04-26 …
在氯,氧两种元素组成的某种化合物中,氧元素的质量分数为47.4%.该化合物与氢氧化钠反应生成两种含 2020-05-13 …
为了测定某铜铁合金(铜铁混合物)中铁的质量分数,某同学利用该合金与稀硫酸反应进行了三次实验,所得相 2020-05-14 …
关于化学分子活化能的疑问(高中)课本上的定义是:活化分子的平均能量与反应物分子平均能量的差值即为活 2020-05-17 …
某密闭容器中进行如下反应:X(g)+2Y(g)==2Z(g),若最初时只加X,Y两种物质,某密闭容 2020-06-07 …
下表是某网络公司员工月收入情况表.月收入(元)45000170001000056005000380 2020-06-08 …
某一反应体系中存在以下五种物质:Na3AsO3、H2O、I2、Na3AsO4、HI.(1)用这五种物 2020-10-30 …
(2008•郑州一模)某一反应体系中存在以下五种物质:Na3AsO3、H2O、I2、Na3AsO4、 2020-10-30 …
为测定某锌铜合金中锌的含量,称取该合金样品进行如图所示实验,发生反应的化学方程式是Zn+H2SO4Z 2020-11-01 …
有一金属元素M它在某些化合物中为+2价,在某些化合物中+3价,单质M与硫粉混合加热,剧烈反应生成黑色 2020-11-22 …