早教吧作业答案频道 -->物理-->
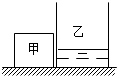
如图所示,密度为5×103千克/米3,边长为0.2米均匀正方体甲和底面积为9×10-2米2的薄壁柱形容器乙放平地面上.乙容器足够高,内盛有0.1米深的水.(1)求甲的质量m甲;(2)求水对乙容器
题目详情
如图所示,密度为5×103千克/米3,边长为0.2米均匀正方体甲和底面积为9×10-2米2的薄壁柱形容器乙放平地面上.乙容器足够高,内盛有0.1米深的水.
(1)求甲的质量m甲;
(2)求水对乙容器底部的压强p乙;
(3)现将甲浸入水中,求水对乙容器底部压强增加量△p乙.

(1)求甲的质量m甲;
(2)求水对乙容器底部的压强p乙;
(3)现将甲浸入水中,求水对乙容器底部压强增加量△p乙.
▼优质解答
答案和解析
(1)甲物体的体积为:
V甲=a甲3=(0.2m)3=8×10-3m3,
根据ρ=
可得甲物体的质量为:
m甲=ρ甲V甲=5×103kg/m3×8×10-3m3=40kg;
(2)水对容器底部的压强为:
p水=ρ水gh=1×103kg/m3×10N/kg×0.1m=1000Pa;
(3)原来水的体积:V水=S容h水=9×10-2m2×0.1m=9×10-3m3,
将甲浸入水中,由于甲的密度大于水的密度,故甲只能沉底.
正方体甲的底面积:S甲=a2=(0.2m)2=4×10-2m2,
正方体甲的高为0.2m,当水恰好能够淹没正方体甲时,如图1,
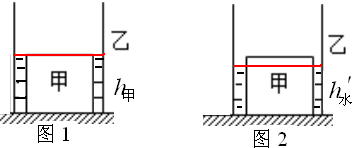
则需要水的体积为:V水′=(S容-S甲)h甲=(9×10-2m2-4×10-2m2)×0.2m=1×10-2m3,
9×10-3m3<1×10-2m3,即V水<V水′,所以水不能淹没正方体甲,如图2,
此时水的深度:h水′=
=
=0.18m,
则水面上升的高度:△h=h水′-h水=0.18m-0.1m=0.08m,
水对容器底部压强增大量:△p乙=ρ水g△h=1×103kg/m3×10N/kg×0.08m=800pa.
答:(1)甲的质量m甲是40kg;
(2)水对乙容器底部的压强p乙为1000pa;
(3)现将甲浸入水中,求水对乙容器底部压强增加量△p乙为800pa.
(1)甲物体的体积为:
V甲=a甲3=(0.2m)3=8×10-3m3,
根据ρ=
| m |
| V |
m甲=ρ甲V甲=5×103kg/m3×8×10-3m3=40kg;
(2)水对容器底部的压强为:
p水=ρ水gh=1×103kg/m3×10N/kg×0.1m=1000Pa;
(3)原来水的体积:V水=S容h水=9×10-2m2×0.1m=9×10-3m3,
将甲浸入水中,由于甲的密度大于水的密度,故甲只能沉底.
正方体甲的底面积:S甲=a2=(0.2m)2=4×10-2m2,
正方体甲的高为0.2m,当水恰好能够淹没正方体甲时,如图1,

则需要水的体积为:V水′=(S容-S甲)h甲=(9×10-2m2-4×10-2m2)×0.2m=1×10-2m3,
9×10-3m3<1×10-2m3,即V水<V水′,所以水不能淹没正方体甲,如图2,
此时水的深度:h水′=
| V水 |
| S容-S甲 |
| 9×10-3m3 |
| 9×10-2m2-4×10-2m2 |
则水面上升的高度:△h=h水′-h水=0.18m-0.1m=0.08m,
水对容器底部压强增大量:△p乙=ρ水g△h=1×103kg/m3×10N/kg×0.08m=800pa.
答:(1)甲的质量m甲是40kg;
(2)水对乙容器底部的压强p乙为1000pa;
(3)现将甲浸入水中,求水对乙容器底部压强增加量△p乙为800pa.
看了如图所示,密度为5×103千克...的网友还看了以下:
设在区间[0,1]上f''(x)>0,则f'(0)f'(1)和f(1)-f(0)的大小顺序是设在区 2020-06-08 …
设f(x),g(x)在[0,1],上的导数连续,且f(0)=0,f'(x),g'(x)>=0.证明 2020-06-11 …
求f(x)=x/(x^2+x-1)在[0,1]上的最大值为什么这样不对:f`(x)=(-x^2-1 2020-06-14 …
f(x)在[0,1]上连续,(0,1)上可导,上f(0)=f(1)=0,证明对任意X0属于(0,1 2020-07-12 …
F(x)在[0,1]上二阶可导,且limx->0f(x)/x=1,limx->1f(x)/x-1= 2020-07-26 …
如何证明单峰函数?设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0 2020-07-30 …
不定积分题和其他题.F(x)在[0,1]上二阶可导,且limx->0f(x)/x=1,limx-> 2020-07-30 …
微积分设函数f(x)在[0,1]上连续,在(0,1)内可导,有f(0)=f(1)=0.证明:至少微 2020-07-31 …
已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1.证明:(已知函 2020-11-02 …
f(x)在[0,1]上二阶可微且f'(0)=f'(1)=0,则存在c,使得f''(c)≥4|f(1) 2020-11-03 …