早教吧作业答案频道 -->数学-->
如图,一次函数y=ax+b的图象与反比例函数y=kx的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).(1)利用图中条件,求反比例函数的解析式和m的值;(2)双
题目详情
如图,一次函数y=ax+b的图象与反比例函数y=
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
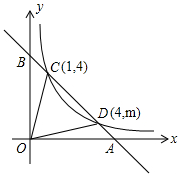
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
| k |
| x |

(1)利用图中条件,求反比例函数的解析式和m的值;
(2)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
▼优质解答
答案和解析
(1)把C(1,4)代入y=
,
得k=4,
把(4,m)代入y=
,得m=1;
∴反比例函数的解析式为y=
,m=1;
把C(1,4),D(4,1)代入y=ax+b得出
,
解得
,
∴一次函数的解析式为y=-x+5;
(2)双曲线上存在点P(2,2),使得S△POC=S△POD,理由如下:
∵C点坐标为:(1,4),D点坐标为:(4,1),
∴OD=OC=
,
∴当点P在∠COD的平分线上时,∠COP=∠POD,又OP=OP,
∴△POC≌△POD,
∴S△POC=S△POD.
∵C点坐标为:(1,4),D点坐标为:(4,1),
可得∠COB=∠DOA,
又∵这个点是∠COD的平分线与双曲线的y=
交点,
∴∠BOP=∠POA,
∴P点横纵坐标坐标相等,
即xy=4,x2=4,
∴x=±2,
∵x>0,
∴x=2,y=2,
故P点坐标为(2,2),使得△POC和△POD的面积相等.
利用点CD关于直线y=x对称,P(2,2)或P(-2,-2).
| k |
| x |
得k=4,
把(4,m)代入y=
| 4 |
| x |
∴反比例函数的解析式为y=
| 4 |
| x |
把C(1,4),D(4,1)代入y=ax+b得出
|
解得
|
∴一次函数的解析式为y=-x+5;
(2)双曲线上存在点P(2,2),使得S△POC=S△POD,理由如下:
∵C点坐标为:(1,4),D点坐标为:(4,1),
∴OD=OC=
| 17 |
∴当点P在∠COD的平分线上时,∠COP=∠POD,又OP=OP,
∴△POC≌△POD,
∴S△POC=S△POD.
∵C点坐标为:(1,4),D点坐标为:(4,1),
可得∠COB=∠DOA,
又∵这个点是∠COD的平分线与双曲线的y=
| 4 |
| x |
∴∠BOP=∠POA,
∴P点横纵坐标坐标相等,
即xy=4,x2=4,
∴x=±2,
∵x>0,
∴x=2,y=2,
故P点坐标为(2,2),使得△POC和△POD的面积相等.
利用点CD关于直线y=x对称,P(2,2)或P(-2,-2).
看了 如图,一次函数y=ax+b的...的网友还看了以下:
已知A+B=2,AB=1求A方+B方,(A-B)方的值坐等 2020-04-05 …
若已知f(x)=a^(2-3x)(a>0且a≠1),g(x)=a^x(1)求函数f(x)图象恒过定 2020-04-25 …
抛物线y=(k+2)x2-(k+1)x-1与x轴交于AB两点,当抛物线顶点P,在x轴下方,且三角形 2020-05-13 …
若代数式x^2-ax+2y-b+bx^2+3x-3y-1的值与字母x取值无关,求代数式3(a^2- 2020-05-13 …
问一道数学题,坐等回答……若a²-2a-1=0,那么a²/(a²×a²+2a²+1)的值为? 2020-05-21 …
椭圆a的平方分之X的平方+b的平方分之Y的平方=1(a>b>0)与直线X+Y=1交于P,Q两点,且 2020-06-03 …
设函数f(x)=ax5+bx3+cx+1且f(π)=-1,求f(-π)的值,坐等. 2020-06-12 …
将椭圆[x平方/9]+y平方=1的纵坐标伸长为原来的3倍,横坐标...将椭圆[x平方/9]+y平方 2020-06-21 …
如图,一次函数y=x+1与反比例函数y=kx的图象交于A,B两点,已知点A的坐标为(1,a),点B 2020-07-20 …
(2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式(m2−m)(m−2m+1 2020-11-13 …