如图，二次函数y=ax2+bx+c的图象交x轴于A（x1，0），B（x2，0）（x1<x2），交y轴于点C（0，3），其顶点M（1，4）．（1）求二次函数的解析式；（2）E为△BCM的外心，试在x轴上确定一点P，使△

Question

如图，二次函数y=ax²+bx+c的图象交x轴于A（x₁，0），B（x₂，0）（x₁<x₂），交y轴于点C（0，3），其顶点M（1，4）．

（1）求二次函数的解析式；
（2）E为△BCM的外心，试在x轴上确定一点P，使△PCE的周长最短，求P点的坐标．

Answer 1

（1）设二次函数的解析式为y=a（x-1）²+4．
∵点C（0，3）在抛物线y=a（x-1）²+4上，
∴3=a（0-1）²+4，
解得a=-1．
∴二次函数的解析式为y=-（x-1）²+4；

（2）过点M作MH⊥y轴于H，如图，
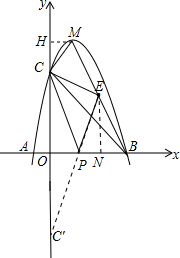则有MH=1，CH=OH-OC=1，
∴MH=CH，
∴∠HMC=∠HCM=45°．
当y=0时，0=-（x-1）²+4，
解得x₁=3，x₂=-1．
∴A（-1，0），B（3，0），
∴OB=OC=3．
∵∠BOC=90°，
∴∠OBC=∠OCB=45°，
∴∠MCB=180°-45°-45°=90°．
∵E为△BCM的外心，
∴点E是BM的中点，
∴点E的坐标为（(1+3)/(2)，(4+0)/(2)），即（2，2）．
作点C关于x轴的对称点C′，连接EC′，交x轴于点P，
则有OC′=0C=3．
根据两点之间线段最短可知：此时PC+PE=PC′+PE最短．
过点E作EN⊥x轴于N，则有ON=2，EN=2，EN∥OC′，
∴△OPC′∽△NPE，
∴(OP)/(PN)=(OC′)/(NE)，
∴(OP)/(2-OP)=(3)/(2)，
解得：OP=1.2，
∴点P的坐标为（1.2，0）．