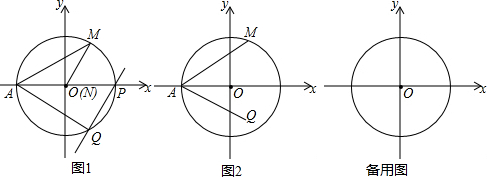
在平面直角坐标系xOy中，半径为1的O与x轴负半轴交于点A，点M在O上，将点M绕点A顺时针旋转60°得到点Q．点N为x轴上一动点（N不与A重合），将点M绕点N顺时针旋转60°得到点P．PQ与x轴所

Question

在平面直角坐标系xOy中，半径为1的 O与x轴负半轴交于点A，点M在 O上，将点M绕点A顺时针旋转60°得到点Q．点N为x轴上一动点（N不与A重合 ），将点M绕点N顺时针旋转60°得到点P．PQ与x轴所夹锐角为α．
（1）如图1，若点M的横坐标为 (1)/(2)，点N与点O重合，则α=___°；
（2）若点M、点Q的位置如图2所示，请在x轴上任取一点N，画出直线PQ，并求α的度数．

Answer 1

（1）如图1，

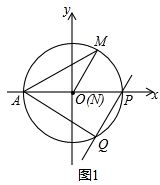
∵∠MOP=60°，
∴∠MAP=30°．
∵∠MAQ=60°，
∴∠QAP=30°．
∵AP是 O的直径，
∴∠AQP=90°，
∴∠APQ=60°，
即α=60°．
故答案为60；

（2）连接MQ，交x轴于E，连接PQ，交x轴于F，连接PM，如图2．

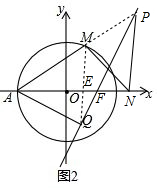
∵点M绕点A顺时针旋转60°得到点Q．
∴△MAQ为等边三角形，
∵点M绕点N顺时针旋转60°得到点P，
∴△MNP为等边三角形，
∴MA=MQ，MN=MP，∠AMQ=∠NMP=60°，
∴∠AMN=∠QMP．
在△AMN和△QMP中，

MA=MQ

∠AMN=∠QMP

MQ=MP

，
∴△AMN≌△QMP（SAS），
∴∠MAN=∠MQP．
∵∠AEQ=∠MAN+∠AMQ，∠AEQ=∠MQP+∠AFQ，
∴∠AFQ=∠AMQ=60°，
∴α的度数为60°．