早教吧作业答案频道 -->数学-->
如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.(Ⅰ)求圆C的方程;(Ⅱ)过点M任作一条直线与椭圆x28+y24=1相交于两点A、B,连接AN、BN,求证
题目详情
如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.
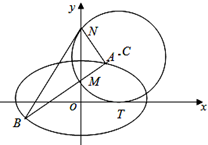
(Ⅰ)求圆C的方程;
(Ⅱ)过点M任作一条直线与椭圆
+
=1相交于两点A、B,连接AN、BN,求证:∠ANM=∠BNM.

(Ⅰ)求圆C的方程;
(Ⅱ)过点M任作一条直线与椭圆
| x2 |
| 8 |
| y2 |
| 4 |
▼优质解答
答案和解析
 (Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r).
(Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r).
∵|MN|=3,∴r2=(
)2+22,解得r2=
,
故圆C的方程为(x-2)2+(y-
)2=
.
(Ⅱ)把x=0代入方程(x-2)2+(y-
)2=
,解得y=1或y=4,
即点M(0,1),N(0,4).
(1)当AB⊥y轴时,由椭圆的对称性可知∠ANM=∠BNM.
(2)当AB与y轴不垂直时,可设直线AB的方程为y=kx+1.
联立方程
,消去y得,(1+2k2)x2+4kx-6=0.
设直线AB交椭圆Γ于A(x1,y1)、B(x2,y2)两点,
则x1+x2=
,x1x2=
.
∴kAN+kBN=
+
=
+
=
=0,
∴∠ANM=∠BNM.
综上所述,∠ANM=∠BNM.
 (Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r).
(Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r).∵|MN|=3,∴r2=(
| 3 |
| 2 |
| 25 |
| 4 |
故圆C的方程为(x-2)2+(y-
| 5 |
| 2 |
| 25 |
| 4 |
(Ⅱ)把x=0代入方程(x-2)2+(y-
| 5 |
| 2 |
| 25 |
| 4 |
即点M(0,1),N(0,4).
(1)当AB⊥y轴时,由椭圆的对称性可知∠ANM=∠BNM.
(2)当AB与y轴不垂直时,可设直线AB的方程为y=kx+1.
联立方程
|
设直线AB交椭圆Γ于A(x1,y1)、B(x2,y2)两点,
则x1+x2=
| -4k |
| 1+2k2 |
| -6 |
| 1+2k2 |
∴kAN+kBN=
| y1-4 |
| x1 |
| y2-4 |
| x2 |
| kx1-3 |
| x1 |
| kx2-3 |
| x2 |
| 2kx1x2-3(x1+x2) |
| x1x2 |
∴∠ANM=∠BNM.
综上所述,∠ANM=∠BNM.
看了 如图,圆C与x轴相切于点T(...的网友还看了以下:
高二数学椭圆问题!已知椭圆方程:x2/4+y2=1.过点Q(-1,0)的直线l交椭圆于A,B两点, 2020-05-15 …
已知椭圆方程3(x^2)+4(y^2)-12=0若直线l:y=mx+m(k≠0),与椭圆交于不同两 2020-05-15 …
已知椭圆方程是x平方/a方+y平方/b方=1,A是椭圆的右顶点,M,N是椭圆上异于A的不同点,且A 2020-06-03 …
已知点F(1,0)为椭圆C:x^2/a^2+y^2/b^2=1的右焦点,过点A(a,0)、B(0, 2020-06-21 …
高数.设方程a0x^n+a1x^(n-1)+...+a(n-1)x=0有一正根x0,证明方程a高数 2020-06-22 …
一个高中数学题 要全解已知椭圆方程(x^2/3b^2)+(y^2/b^2)=1 (b>0),经过椭 2020-06-27 …
已知圆N经过点A(3,1),B(-1,3),且它的圆心在直线3x-y-2=0上.(Ⅰ)求圆N的方程 2020-07-26 …
圆锥曲线解析几何已知椭圆x/a+y/b=1(a>b>0)左焦点F1(-1,0),长轴长与短轴长的比 2020-07-31 …
求解一道解析几何证明题椭圆中焦点三角形F1PF2.D非顶点,角F1DF2的内角平分线和外角平分线分 2020-08-02 …
一道解析几何问题,望答复设椭圆=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点 2020-08-02 …