如图，在平面直角坐标系xOy中，二次函数y=a（x+2）（x-4）（a<0）的图象与x轴交于A，B两点（点A在点B的左侧），顶点为M，经过点A的直线l：y=ax+b与y轴交于点C，与抛物线的另一

Question

如图，在平面直角坐标系 xOy 中，二次函数 y=a（x+2）（x-4）（a<0）的图象与 x 轴交于 A，B 两点（点 A 在点 B的左侧），顶点为 M，经过点 A 的直线 l：y=ax+b 与 y 轴交于点 C，与抛物线的另一个交点为 D．

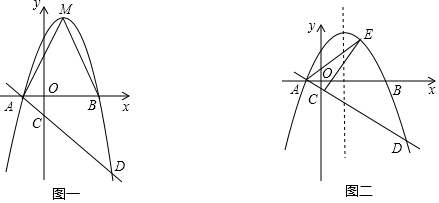
（1）直接写出点 A 的坐标___、点 B 的坐标___；
（2）如图（1），若顶点 M 的坐标为（1，9），连接 BM、AM、BD，请求出二次函数及一次函数的解析式，并求出四边形 ADBM 的面积；
（3）如图（2），点 E 是直线 l 上方的抛物线上的一点，若△ACE 的面积的最大值为 (49)/(4)时，请直接写出此时 E 点的坐标．

Answer 1

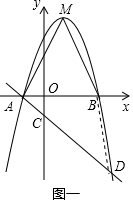（1）如图一，令 y=0，则a（x+2）（x-4）=0，
解得x₁=-2，x₂=4，
所以A（-2，0），B（4，0）．
故答案为：A（-2，0）；（ 4，0）；

（2）如图一，连接BD．
∵二次函数 y=a（x+2）（x-4）顶点为（1，9），带入即可求得 a=1．
∴抛物线为 y=-x²+2x+8，
∵一次函数 y=ax+b 经过 A（-2，0），
∴2=-a+b，
∴b=a，
∴一次函数为：y=-x-2，联立一次函数与二次函数解析式可求 D（4-7）；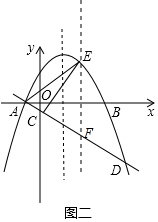
S_{四边形ADBM}=S_△ABM+S_△ABD=(1)/(2)×6×9+(1)/(2)×6×7=48．

（3）如图二，过 点 E 作 EF∥y 轴，交 直 线 AD 于 点 F，设 E（x，ax²-2ax-8a），则
F（x，ax+2a），EF=ax²-2ax-8a-（ax+a）=ax²-3ax-10a，
∵S_ACE=S_AFE-S_△CFE=(1)/(2)（ax²-3ax-10a）⋅（x+1）-(1)/(2)（ax²-3ax-10a）⋅x=(1)/(2)（ax²-3ax-10a）=(1)/(2)（ax²-3ax-10a）
∴当 x=(3)/(2)时，△ACE 面积最大值=(-49)/(8a)=(49)/(4)，
∴a=-2，
∴此时点 E((3)/(2)，(35)/(2))．