早教吧作业答案频道 -->数学-->
如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.(1)求证:BD=AC;(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.①如图②,当点F落在AC上时,
题目详情
如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.
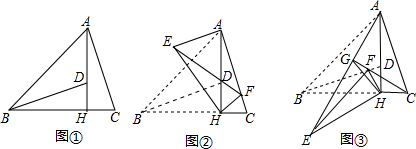
(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
①如图②,当点F落在AC上时,(F不与C重合),若BC=4,tanC=3,求AE的长;
②如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.

(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
①如图②,当点F落在AC上时,(F不与C重合),若BC=4,tanC=3,求AE的长;
②如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
▼优质解答
答案和解析
(1)在Rt△AHB中,∠ABC=45°,
∴AH=BH,
在△BHD和△AHC中,
,
∴△BHD≌△AHC,
∴BD=AC,
(2)①如图,
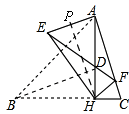
在Rt△AHC中,
∵tanC=3,
∴
=3,
设CH=x,
∴BH=AH=3x,
∵BC=4,
∴3x+x=4,
∴x=1,
∴AH=3,CH=1,
由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHA=∠FHC,
=
=1,
∴△EHA∽△FHC,
∴∠EAH=∠C,
∴tan∠EAH=tanC=3,
过点H作HP⊥AE,
∴HP=3AP,AE=2AP,
在Rt△AHP中,AP2+HP2=AH2,
∴AP2+(3AP)2=9,
∴AP=
,
∴AE=
;
②如图③,
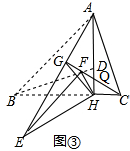
由①有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQE,
∴△AQC∽△GQH,
∴
=
=
=
=2.
∴AH=BH,
在△BHD和△AHC中,
|
∴△BHD≌△AHC,
∴BD=AC,
(2)①如图,

在Rt△AHC中,
∵tanC=3,
∴
| AH |
| CH |
设CH=x,
∴BH=AH=3x,
∵BC=4,
∴3x+x=4,
∴x=1,
∴AH=3,CH=1,
由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHA=∠FHC,
| EH |
| AH |
| FH |
| HC |
∴△EHA∽△FHC,
∴∠EAH=∠C,
∴tan∠EAH=tanC=3,
过点H作HP⊥AE,
∴HP=3AP,AE=2AP,
在Rt△AHP中,AP2+HP2=AH2,
∴AP2+(3AP)2=9,
∴AP=
3
| ||
| 10 |
∴AE=
3
| ||
| 5 |
②如图③,

由①有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQE,
∴△AQC∽△GQH,
∴
| EF |
| HG |
| AC |
| GH |
| AQ |
| GQ |
| 1 |
| sin30° |
看了 如图①,△ABC中,∠ABC...的网友还看了以下:
在正三棱锥P-ABC,AB=PA=8,过A作与PB,PC分别交于D和E的截面,则截面三角形ADE的 2020-05-14 …
如图,一次函数y1=ax+b与x轴,y轴分别交于D,C两点,与反比例函数Y2=k/x交于A(1,3 2020-05-17 …
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙ 2020-06-16 …
如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D、E两点.(1 2020-07-14 …
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线(a≠0,x>0)分别交于D、E两点.(1 2020-07-14 …
如图,已知矩形OABC中,OA=3,AB=4,双曲线y=kx(k>0)与矩形两边AB、BC分别交于 2020-07-21 …
如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y=kx(x>0)的图 2020-07-22 …
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC= 2020-08-01 …
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC= 2020-08-01 …
如图,已知椭圆C:x2a2+y2b2=1,其左右焦点为F1(-1,0)及F2(1,0),过点F1的直 2020-11-27 …