早教吧作业答案频道 -->数学-->
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=22,AC=4(I)求证:EG∥CO;(Ⅱ)求BC的长.
题目详情
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2
,AC=4
(I)求证:EG∥CO;
(Ⅱ)求BC的长.
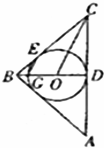
| 2 |
(I)求证:EG∥CO;
(Ⅱ)求BC的长.
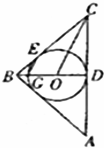
▼优质解答
答案和解析
(Ⅰ)证明:连结DE,∵BC=BA,∴∠CBA的平分线与AC边上的中线重合,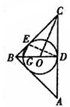
三角形的内切圆的圆心是三条角平分线的交点,
∴圆心O在直线BD上,
∴GD为圆O的直径,∴EG⊥ED,∴CO是∠ECD的角平分线,
又 O与AC、BC分别相切于D、E两点,
∴CE=CD,∴ED⊥CO,
∴EG∥CO.
(Ⅱ) 由(Ⅰ)知:AD=DC=
AC=2,且∠BDC=90°,
在Rt△BDC中,由勾股定理得:BD2=BC2-CD2=(2
)2-22=4,
∴BD=2,
由圆的切线长定理,得CE=CD=2,
∴BE=2
-2,
由切割线定理得BE2=BG•BD,即(2
-2)2=BG•2,
解得BG=6-4
.

三角形的内切圆的圆心是三条角平分线的交点,
∴圆心O在直线BD上,
∴GD为圆O的直径,∴EG⊥ED,∴CO是∠ECD的角平分线,
又 O与AC、BC分别相切于D、E两点,
∴CE=CD,∴ED⊥CO,
∴EG∥CO.
(Ⅱ) 由(Ⅰ)知:AD=DC=
| 1 |
| 2 |
在Rt△BDC中,由勾股定理得:BD2=BC2-CD2=(2
| 2 |
∴BD=2,
由圆的切线长定理,得CE=CD=2,
∴BE=2
| 2 |
由切割线定理得BE2=BG•BD,即(2
| 2 |
解得BG=6-4
| 2 |
看了 已知圆O是△ABC的内切圆,...的网友还看了以下:
如图,角B=90℃,AB=BC =4,AD =2,CD =6.(1)求AC的长(2)请判断三角形A 2020-05-16 …
如图AC垂直于BC,CD垂直于AB,角1=角2,则下列结论中正确的有()①角1=角B②角3=角A③ 2020-05-17 …
已知三角形ABC,D是BC边上一点,向量AD=λ(AB/|AB|+AC/|AC|),|),|AB| 2020-06-06 …
(2014•陕西)设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为 2020-06-10 …
如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合), 2020-06-12 …
3.曲线y=3x2-x3+x-7的拐点是A.(1,4)B.1C.-4D.(1,4)2.设有一块边长 2020-06-22 …
一阶矩阵的逆矩阵是什么,如[4][a]^(-1)=1/a是不是如果a不等于0的情况下,都是1/a? 2020-06-30 …
如图,已知AB=AC,∠A=36°,AB的中垂线MD交AC于点D,交AB于点M.下列结论:1、BD 2020-08-01 …
设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2 2020-10-31 …
如图已知△ABC中,DE//BC,点D,E分别在边AB,AC上.(1)如果AD=5,DB=3,AE= 2020-11-11 …