早教吧作业答案频道 -->数学-->
在平面直角坐标系中,O为坐标原点,直线y=-x+6与x轴交于点A,与y轴交于点B,抛物线y=ax2-6ax过线O、A交直线AB于点C,且C点的纵坐标比横坐标大4.(1)如图1,求a的值;(2)如图2,动点D在线
题目详情
在平面直角坐标系中,O为坐标原点,直线y=-x+6与x轴交于点A,与y轴交于点B,抛物线y=ax2-6ax过线O、A交直线AB于点C,且C点的纵坐标比横坐标大4.
(1)如图1,求a的值;
(2)如图2,动点D在线段OB上,点E在线段AB上,DE∥x,点F在线段DC的延长线上,EF∥y轴,交x轴于点G,当点F恰好落在抛物线上时,求点D、F的坐标;
(3)在(2)的条件下,点P在第一象限内的抛物线上,PH⊥CD于点H,若tan∠FPH=
,求点P的坐标.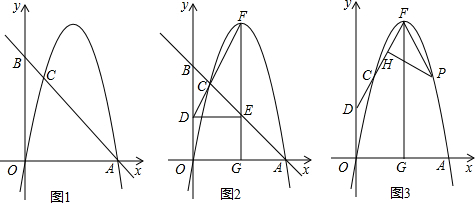
(1)如图1,求a的值;
(2)如图2,动点D在线段OB上,点E在线段AB上,DE∥x,点F在线段DC的延长线上,EF∥y轴,交x轴于点G,当点F恰好落在抛物线上时,求点D、F的坐标;
(3)在(2)的条件下,点P在第一象限内的抛物线上,PH⊥CD于点H,若tan∠FPH=
| 3 |
| 4 |

▼优质解答
答案和解析
设C(x,-x+6),
∵C点的纵坐标比横坐标大4,
∴x+4=-x+6,
∴x=1,
∴C(1,5),
∵点C在抛物线y=ax2-6ax上,
∴a-6a=5,
∴a=-1,
(2)设D(0.m)
∵C(1,5),
∴直线CD解析式为y=(5-m)x+m,
∵DE∥x轴,
∴E的纵坐标为m,
∵点E在y=-x+6上,
∴E(6-m,m)
∴点F的横坐标为6-m,
∵点F在直线CD解析式为y=(5-m)x+m上,
∴F(6-m,m2-10m+30),
由(1)得,抛物线解析式为y=-x2+6x,
∴m2-10m+30=-(6-m)2+6(6-m),
∴m=5(舍)或m=3,
∴D(0,3),F(3,9),
(3)如图,
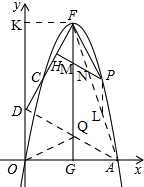
过点F作FK⊥y轴,连接AD,AF,AF交PH于N,PH交PG于M,过点P作PL⊥y轴交AF于L,
∵F(3,9),D(0,3),A(6,0),
∴FK=OD=3,DK=OA=6,
∵∠FKD=∠DOA=90°,
∴△FKD≌△DOA,
∴∠DFK=∠ADO,AD=DF,
∵∠DFK+∠KDF=90°,
∴∠ADO+∠HDF=90°,
∴∠ADF=180°-90°=90°,
∴△ADF是等腰直角三角形,
∵PH⊥CD,
∴PH∥AD,
∴∠AFD=45°,
设AD交FG于Q,
∵G(3,0),A(6,0),
∴OG=AG,
∵FG∥y轴,
∴AQ=OQ,
∵PH∥AD,
∴
=
=
,
∴HM=MN,
∵∠AFD=45°,
∴CF=HN,
∵tan∠FPH=
=
,
∴PN=
MN,
∵PL∥FH,
∴
=
=
,
∵F(3,9),A(6,0),D(0,3),
∴直线AD解析式为y=-
x+3,
直线AF解析式为y=-3x+18,
设P(t,-t2+6t),
∴直线PH解析式为y=-
x-t2+
t,
∴M(3,-t2+
t-
),
∴FM=9-(-t2+
t-
)=t2-
t+
,
∵PL=-t2+9t-18,
∴3(-t2+9t-18)=2(t2-
t+
),
∴t=3(舍)或t=5,
∴P(5,5).
∵C点的纵坐标比横坐标大4,
∴x+4=-x+6,
∴x=1,
∴C(1,5),
∵点C在抛物线y=ax2-6ax上,
∴a-6a=5,
∴a=-1,
(2)设D(0.m)
∵C(1,5),
∴直线CD解析式为y=(5-m)x+m,
∵DE∥x轴,
∴E的纵坐标为m,
∵点E在y=-x+6上,
∴E(6-m,m)
∴点F的横坐标为6-m,
∵点F在直线CD解析式为y=(5-m)x+m上,
∴F(6-m,m2-10m+30),
由(1)得,抛物线解析式为y=-x2+6x,
∴m2-10m+30=-(6-m)2+6(6-m),
∴m=5(舍)或m=3,
∴D(0,3),F(3,9),
(3)如图,

过点F作FK⊥y轴,连接AD,AF,AF交PH于N,PH交PG于M,过点P作PL⊥y轴交AF于L,
∵F(3,9),D(0,3),A(6,0),
∴FK=OD=3,DK=OA=6,
∵∠FKD=∠DOA=90°,
∴△FKD≌△DOA,
∴∠DFK=∠ADO,AD=DF,
∵∠DFK+∠KDF=90°,
∴∠ADO+∠HDF=90°,
∴∠ADF=180°-90°=90°,
∴△ADF是等腰直角三角形,
∵PH⊥CD,
∴PH∥AD,
∴∠AFD=45°,
设AD交FG于Q,
∵G(3,0),A(6,0),
∴OG=AG,
∵FG∥y轴,
∴AQ=OQ,
∵PH∥AD,
∴
| HM |
| DQ |
| FM |
| FQ |
| MN |
| AQ |
∴HM=MN,
∵∠AFD=45°,
∴CF=HN,
∵tan∠FPH=
| HF |
| HP |
| 3 |
| 4 |
∴PN=
| 2 |
| 3 |
∵PL∥FH,
∴
| PL |
| PM |
| PN |
| MN |
| 2 |
| 3 |
∵F(3,9),A(6,0),D(0,3),
∴直线AD解析式为y=-
| 1 |
| 2 |
直线AF解析式为y=-3x+18,
设P(t,-t2+6t),
∴直线PH解析式为y=-
| 1 |
| 2 |
| 13 |
| 2 |
∴M(3,-t2+
| 13 |
| 2 |
| 3 |
| 2 |
∴FM=9-(-t2+
| 13 |
| 2 |
| 3 |
| 2 |
| 13 |
| 2 |
| 21 |
| 2 |
∵PL=-t2+9t-18,
∴3(-t2+9t-18)=2(t2-
| 13 |
| 2 |
| 21 |
| 2 |
∴t=3(舍)或t=5,
∴P(5,5).
看了 在平面直角坐标系中,O为坐标...的网友还看了以下:
如果想新增一个FTP站点,则单击“Add Site”,会弹出一个对话框,那么在站点标签中需要填入的信 2020-05-26 …
起点在坐标原点的向量叫做定位向量或位置向量,其坐标等于它的什么坐标;向量的坐标等于它的什么坐标减. 2020-06-14 …
1、在一个圆上标出一些数,第一次先把圆周分成二等分,在两个分点分别标上1和2;第二次把两段半圆弧分 2020-06-18 …
在线段AB上,先在A点点标注0,在B点标注2002,这次称为第一次操作;然后在AB中点C处标注(0 2020-06-30 …
在线段AB上,先在A点标注0,在B点标注2002,这称为第一次操作,然后在AB的中点C处标注(0+ 2020-06-30 …
在直角坐标系中,已知直线L是第一、三象限的角平分线.小题如下①若点A的坐标(3,1),在坐标系中描 2020-07-19 …
在线段AB上,先在A点标注0,在B点标注2002,这称为第一次操作;然后再在AB的中点C处标注(0 2020-07-21 …
4.在一个圆上标出一些数:第一次先把圆周二等分,在两个分点分别标上2和4.第二次把两段半弧分别二等分 2020-11-19 …
西铁城表盘编号西铁城的表盘6点位置的编号是独一无二的吗?与背面的编号一样吗JY0005-50E这款表 2020-11-29 …
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点4230N1N2N3N直角坐标系中,矩 2020-12-25 …