早教吧作业答案频道 -->数学-->
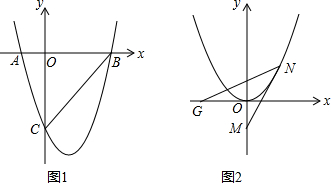
如图1,抛物线y=ax2+bx-3与y轴于点,与x轴交于A、B两点,OB=3OA,∠ABC=45°(1)求此抛物线的解析式;(2)如图2,平移此抛物线使其顶点为坐标原点,点M为y轴上一动点,MN与抛物线只有唯一公
题目详情
如图1,抛物线y=ax2+bx-3与y轴于点,与x轴交于A、B两点,OB=3OA,∠ABC=45°
(1)求此抛物线的解析式;
(2)如图2,平移此抛物线使其顶点为坐标原点,点M为y轴上一动点,MN与抛物线只有唯一公共点N点,点G在x轴上,∠GNM=∠OMN,求证:直线NG必过一定点,并求此定点的坐标.
(1)求此抛物线的解析式;
(2)如图2,平移此抛物线使其顶点为坐标原点,点M为y轴上一动点,MN与抛物线只有唯一公共点N点,点G在x轴上,∠GNM=∠OMN,求证:直线NG必过一定点,并求此定点的坐标.

▼优质解答
答案和解析
(1)由题意OC=OB=3,OA=1,
∴点A坐标(-1,0),点B坐标(3,0),
∴
解得
,
∴抛物线解析式为y=x2-2x-3.
(2)如图2中,平移后的抛物线解析式为y=x2,
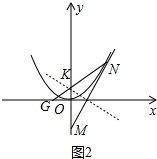
设点M坐标(0,b),直线MN解析式为y=kx+b,
由
消去y得到x2-kx-b=0,由题意△=0,
∴k2+4b=0,
b=-
,
∴点M坐标(0,-
),N(
,
),
线段MN中点G坐标为(
,0),
设过点G垂直MN的直线的解析式为y=-
x+b′,把(
,0)代入得到b′=
,
∴该直线解析式为y=-
x+
,该直线与y轴交于点K(0,
),
连接KN,则有KM=KN,
∴∠KNM=∠KMO,∵∠GNM=∠OMN
∴点K在直线GN上,直线GN经过定点(0,
).
∴点A坐标(-1,0),点B坐标(3,0),
∴
|
|
∴抛物线解析式为y=x2-2x-3.
(2)如图2中,平移后的抛物线解析式为y=x2,

设点M坐标(0,b),直线MN解析式为y=kx+b,
由
|
∴k2+4b=0,
b=-
| k2 |
| 4 |
∴点M坐标(0,-
| k2 |
| 4 |
| k |
| 2 |
| k2 |
| 4 |
线段MN中点G坐标为(
| k |
| 4 |
设过点G垂直MN的直线的解析式为y=-
| 1 |
| k |
| k |
| 4 |
| 1 |
| 4 |
∴该直线解析式为y=-
| 1 |
| k |
| 1 |
| 4 |
| 1 |
| 4 |
连接KN,则有KM=KN,
∴∠KNM=∠KMO,∵∠GNM=∠OMN
∴点K在直线GN上,直线GN经过定点(0,
| 1 |
| 4 |
看了 如图1,抛物线y=ax2+b...的网友还看了以下:
2007年江苏省苏州市中考数学最后一题的第三小题设抛物线y=ax2+bx-2与x轴交于两个不同的点 2020-04-25 …
已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).(Ⅰ)求实数a 2020-05-17 …
已知抛物线y=ax2+x+2.(1)当a=-1时,求此抛物线的顶点坐标和对称轴;(2)若代数式-x 2020-05-17 …
设f(x)为连续函数,f(0)=a,F(t)=∫∫∫Ω{z-f(x^2+y^2+z^2)]dv,其 2020-06-15 …
已知y-2与x成正比,且当x=1时,y=-6,求y与x之间的函数关系式 若点(a,2)在这个函数已 2020-06-27 …
(2010•同安区质检)已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6, 2020-08-03 …
几道初二数学题目!~~~~1.已知y-2与x成正比例关系,且当x=1时y=6.(1)求x与y之间的函 2020-11-07 …
(2006•湛江)已知抛物线y=ax2+bx+2与x轴相交于点A(x1,0),B(x2,0)(200 2020-11-12 …
当x=0,y=1时,x^2-2xy+y^2与(x-y)^2的值相同吗?当x=-1,y=-2时呢?否无 2020-12-31 …
已知y+2与x成正比例,且x=-2时,y=0.设点P在y轴负半轴上,(2)中的图像与x轴、y轴分别交 2021-01-11 …