早教吧作业答案频道 -->数学-->
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.(1)求抛物线的解析式
题目详情
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
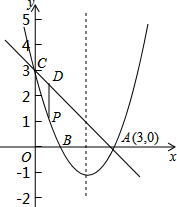
(1)求抛物线的解析式;
(2)当D在线段AC上运动时,求点P在运动的过程中线段PD长度的最大值;
(3)在抛物线对称轴上是否存在点M使|MA-MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
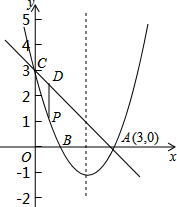
(1)求抛物线的解析式;
(2)当D在线段AC上运动时,求点P在运动的过程中线段PD长度的最大值;
(3)在抛物线对称轴上是否存在点M使|MA-MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
▼优质解答
答案和解析
(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
∴
,
解得
,
∴抛物线解析式为y=x2-4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=-x+3,
设点P(x,x2-4x+3),
∵PD∥y轴,
∴点D(x,-x+3),
∴PD=(-x+3)-(x2-4x+3)=-x2+3x=-(x-
)2+
,
∵a=-1<0,
∴当x=
时,线段PD的长度有最大值
;
(3)由抛物线的对称性,对称轴垂直平分AB,
∴MA=MB,
由三角形的三边关系,|MA-MC|<BC,
∴当M、B、C三点共线时,|MA-MC|最大,为BC的长度,
设直线BC的解析式为y=kx+b(k≠0),
则
,
解得
,
∴直线BC的解析式为y=-3x+3,
∵抛物线y=x2-4x+3的对称轴为直线x=2,
∴当x=2时,y=-3×2+3=-3,
∴点M(2,-3),
即,抛物线对称轴上存在点M(2,-3),使|MA-MC|最大.
∴
|
解得
|
∴抛物线解析式为y=x2-4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=-x+3,
设点P(x,x2-4x+3),
∵PD∥y轴,
∴点D(x,-x+3),
∴PD=(-x+3)-(x2-4x+3)=-x2+3x=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
∵a=-1<0,
∴当x=
| 3 |
| 2 |
| 9 |
| 4 |
(3)由抛物线的对称性,对称轴垂直平分AB,
∴MA=MB,
由三角形的三边关系,|MA-MC|<BC,
∴当M、B、C三点共线时,|MA-MC|最大,为BC的长度,
设直线BC的解析式为y=kx+b(k≠0),
则
|
解得
|
∴直线BC的解析式为y=-3x+3,
∵抛物线y=x2-4x+3的对称轴为直线x=2,
∴当x=2时,y=-3×2+3=-3,
∴点M(2,-3),
即,抛物线对称轴上存在点M(2,-3),使|MA-MC|最大.
看了 如图,抛物线y=x2+bx+...的网友还看了以下:
如图,已知二次函数y=x+bx+c过点A(1,0)(1)求此二次函数的解析式(2)在抛物线上如图, 2020-04-26 …
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C(1)求抛 2020-05-15 …
点M(4,0)以点M为圆心、2为半径的圆与x轴交与点A,B,已知抛物线y=1/6x^2+bx+c过 2020-05-16 …
如图,在直角坐标平面内,O为原点,抛物线y=ax2+bx经过点A(6,0),且顶点B(m,6)在直 2020-06-12 …
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点 2020-07-26 …
根据下列条件分别确定二次函数的解析式抛物线y=ax^2+bx+c过点(-3.2)(-1.-1)(1 2020-08-01 …
在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(-3,4),直线l与x轴相交于点B,与∠A 2020-11-01 …
已知抛物线y=x方+bx+3a,过点A(1,0)B(0,-3)与x轴交于另一点c.已知抛物线y=x方 2020-11-27 …
九年级下第二十六章复习题26第六题6.根据下列条件,分别确定二次函数的解析式:(1)抛物线y=ax^ 2020-12-13 …
已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动 2021-01-12 …