早教吧作业答案频道 -->数学-->
如图(1),抛物线y=x2+x-4与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线y=x+b与抛物线交于点B、C.(1)求点A的坐标;(2)当b=0时(如图(2)),△ABE与△ACE的面积大小关系
题目详情
如图(1),抛物线y=x 2 +x-4与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线y=x+b与抛物线交于点B、C.
(1)求点A的坐标;
(2)当b=0时(如图(2)),△ABE与△ACE的面积大小关系如何?当b>-4时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC为斜边的直角三角形?若存在,求出b;若不存在,说明理由.
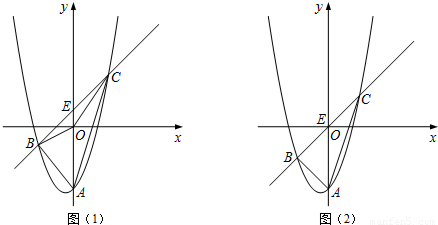
(1)求点A的坐标;
(2)当b=0时(如图(2)),△ABE与△ACE的面积大小关系如何?当b>-4时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC为斜边的直角三角形?若存在,求出b;若不存在,说明理由.

▼优质解答
答案和解析
【答案】分析:(1)知道抛物线的解析式,要求与y轴的交点,令x=0就能求得.(2)当b=0时,直线为y=x,联立两方程式解得交点坐标,由三角形面积公式分别求出两三角形的面积.当b>-4时,仍然联立方程解坐标,作BF⊥y轴,CG⊥y轴,垂足分别为F、G,解得BF和CG的值,再由面积公式求面积值.(3)由BF=CG,∠BEF=∠CEG,∠BFE=∠CGE=90°,可证△BEF≌△CEG,可知BE=CE,即E为BC的中点,当OE=CE时,△OBC为直角三角形,解三角形得到答案.(1)将x=0,代入抛物线解析式,得点A的坐标为(0,-4),(2)当b=0时,直线为y=x,由,解得,.∴B、C的坐标分别为(-2,-2),(2,2),,∴S△ABE=S△ACE.当b>-4时,仍有S△ABE=S△ACE成立.理由如下由,解得,.故B、C的坐标分别为(-,-+b),(,+b),作BF⊥y轴,CG⊥y轴,垂足分别为F、G,则,而△ABE和△ACE是同底的两个三角形,∴S△ABE=S△ACE.(3)存在这样的b,∵BF=CG,∠BEF=∠CEG,∠BFE=∠CGE=90°,∴△BEF≌△CEG,∴BE=CE,即E为BC的中点,∴当OE=CE时,OE=BC,此时△OBC为直角三角形.∵,∴,而OE=|b|,∴,解得b1=4,b2=-2,∴当b=4或-2时,△OBC为直角三角形.点评:本题主要考查二次函数的应用,是一道综合性很强的习题,做题需要细心.
看了 如图(1),抛物线y=x2+...的网友还看了以下:
如图,△ACE是以□ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称。若E点的坐标是( 2020-05-02 …
(2014•福建模拟)如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1 2020-05-15 …
如图,平面直角坐标系中,在第他象限的矩形y四CO的边Oy在y正半轴上,OC在x正半轴上,点D是线段 2020-06-14 …
抛物线y=x2+2x-3与x轴交于A、B两点,与y轴交于C点,点E为x轴上任意一点,在抛物线上是否 2020-06-14 …
已知抛物线y=ax+bx+3与x轴交点于A(1,0)B(-3,0)于y轴交点为C,若点E为第二象限 2020-07-20 …
如图,直角坐标平面xOy中,点A在x轴上,点C与点E在y轴上,且E为OC中点,BC∥x轴,且BE⊥ 2020-07-29 …
已知椭圆C:x24+y2=1的短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F 2020-07-31 …
如图所示的点A、B、C、D、E中,哪两个点关于x轴对称?哪两个点关于y轴对称?点C和点E关于x轴对 2020-08-01 …
八年级函数与几何图形的综合应用在直角坐标系中,点B的坐标为(0,根号3),A点在x轴正半轴,E是线 2020-08-02 …
如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=12x+2经过点B(x,1)与x轴, 2020-11-30 …