早教吧作业答案频道 -->数学-->
在平面直角坐标系中,抛物线y=-12x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.(1)求抛物线的解析式;(2)在AC上方的抛物线上有一动点P.①如图1,当点P运动到某位置时
题目详情
在平面直角坐标系中,抛物线y=-
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
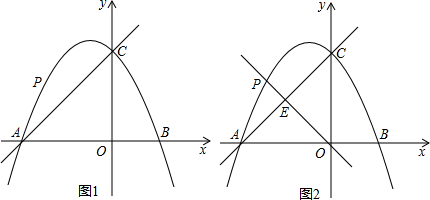
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
| 1 |
| 2 |
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.

▼优质解答
答案和解析
(1)∵直线y=x+4经过A,C两点,
∴A点坐标是(-4,0),点C坐标是(0,4),
又∵抛物线过A,C两点,
∴
,解得:
,
∴抛物线的解析式为y=-
x2-x+4.
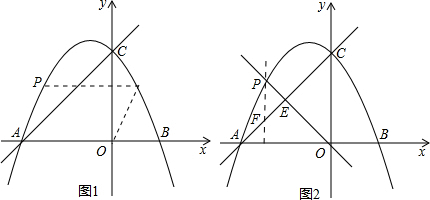
(2)①如图1
∵y=-
x2-x+4,
∴抛物线的对称轴是直线x=-1.
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,
∴PQ∥AO,PQ=AO=4.
∵P,Q都在抛物线上,
∴P,Q关于直线x=-1对称,
∴P点的横坐标是-3,
∴当x=-3时,y=-
×(-3)2-(-3)+4=
,
∴P点的坐标是(-3,
);
②过P点作PF∥OC交AC于点F,
∵PF∥OC,
∴△PEF∽△OEC,
∴
=
.
又∵
=
,OC=4,
∴PF=
,
设点F(x,x+4),
∴(-
x2-x+4)-(x+4)=
,
化简得:x2+4x+3=0,解得:x1=-1,x2=-3.
当x=-1时,y=
;当x=-3时,y=
,
即P点坐标是(-1,
)或(-3,
).
又∵点P在直线y=kx上,
∴k=-
或k=-
.
∴A点坐标是(-4,0),点C坐标是(0,4),
又∵抛物线过A,C两点,
∴
|
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
(2)①如图1
∵y=-
| 1 |
| 2 |
∴抛物线的对称轴是直线x=-1.
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,
∴PQ∥AO,PQ=AO=4.
∵P,Q都在抛物线上,
∴P,Q关于直线x=-1对称,
∴P点的横坐标是-3,
∴当x=-3时,y=-
| 1 |
| 2 |
| 5 |
| 2 |

∴P点的坐标是(-3,
| 5 |
| 2 |
②过P点作PF∥OC交AC于点F,
∵PF∥OC,
∴△PEF∽△OEC,
∴
| PE |
| OE |
| PF |
| OC |
又∵
| PE |
| OE |
| 3 |
| 8 |
∴PF=
| 3 |
| 2 |
设点F(x,x+4),
∴(-
| 1 |
| 2 |
| 3 |
| 2 |
化简得:x2+4x+3=0,解得:x1=-1,x2=-3.
当x=-1时,y=
| 9 |
| 2 |
| 5 |
| 2 |
即P点坐标是(-1,
| 9 |
| 2 |
| 5 |
| 2 |
又∵点P在直线y=kx上,
∴k=-
| 9 |
| 2 |
| 5 |
| 6 |
看了 在平面直角坐标系中,抛物线y...的网友还看了以下:
点A是反比例函数y=2/x(x>0)的图象上的任意一点,AB∥x轴交反比例函数y=-3/x的图像于 2020-04-08 …
1如图,A,B是函数y=k/x的图象上关于原点O对称的任意两点,AP平行于y轴,交x轴于点P,BH 2020-06-12 …
如图,在平面直角坐标系中,函数y=x和函数y=16x的图象在第一象限交于点D(4,m),与平行于y 2020-06-13 …
如图,y轴的负半轴平分∠AOB,P为y轴负半轴上的一动点,过点P作x轴的平行线分别交OA、OB于点 2020-06-29 …
如图,过y轴上一点A(0,1)作AC平行于x轴,交抛物线如图,过y轴上一点A(0,1)作AC平行X 2020-07-29 …
如图,平行于x轴的直线AC分别交抛物线y1=x的平方于y=三分之一x的平方与BC两点,过C作y轴如 2020-07-29 …
如图,点P是函数y=4/x在第一象限的图像上的任意一点,点P关于原点的对称点是P’,过点P做PA平 2020-07-29 …
如图1,点A为抛物线C1:y=x2﹣2的顶点,点B的坐标为(1,0)直线AB交抛物线C1于另一点C( 2020-10-31 …
如图,过点A(8.0),B(0,8√3)两点的直线与直线y=√3x交与点C,平行于y轴的直线l从原点 2021-01-10 …
如图,在平面直角坐标系中,点A、B为正比例函数y=kx(k>0)与反比例函数y=mx(m≠0)的交点 2021-02-04 …