如图，扇形AOD中，∠AOD=90°，OA=6，点P为弧AD上任意一点（不与点A和D重合），PQ⊥OD于Q，点I为△OPQ的内心，过O，I和D三点的圆的半径为r．则当点P在弧AD上运动时，r的值满足（）A.0<r&lt

Question

如图，扇形AOD中，∠AOD=90°，OA=6，点P为弧AD上任意一点（不与点A和D重合），PQ⊥OD于Q，点I为△OPQ的内心，过O，I和D三点的圆的半径为r．则当点P
在弧AD上运动时，r的值满足（　　）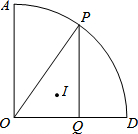

A. 0<r<3

B. r=3

C. 3<r<3

√(2)

D. r=3

√(2)

Answer 1

如图，连OI，PI，DI，
∵△OPH的内心为I，
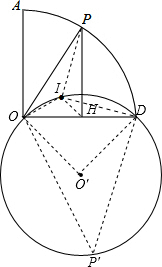
∴∠IOP=∠IOD，∠IPO=∠IPH，
∴∠PIO=180°-∠IPO-∠IOP=180°-(1)/(2)（∠HOP+∠OPH），
而PH⊥OD，即∠PHO=90°，
∴∠PIO=180°-(1)/(2)（∠HOP+∠OPH）=180°-(1)/(2)（180°-90°）=135°，
在△OPI和△ODI中，

IO=IO

∠POI=∠DOI

OD=OP

，
∴△OPI≌△ODI（SAS），
∴∠DIO=∠PIO=135°，
所以点I在以OD为弦，并且所对的圆周角为135°的一段劣弧上；
过D、I、O三点作 O′，如图，连O′D，O′O，
在优弧DO取点P′，连P′D，P′O，
∵∠DIO=135°，
∴∠DP′O=180°-135°=45°，
∴∠DO′O=90°，而OD=6，
∴OO′=DO′=3√(2)，
∴r的值为3√(2)．
故选：D．