早教吧作业答案频道 -->数学-->
如图,已知点D在反比例函数y=mx的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=23.(1)求反比例函数y=mx和直线y=kx+b的解析式;(2
题目详情
如图,已知点D在反比例函数y=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
.
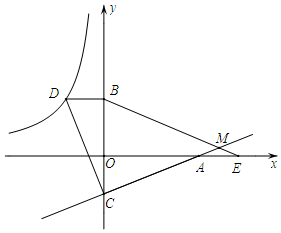
(1)求反比例函数y=
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
| m |
| x |
| 2 |
| 3 |

(1)求反比例函数y=
| m |
| x |
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
▼优质解答
答案和解析
(1)∵A(5,0),
∴OA=5.
∵tan∠OAC=
,
∴
=
,解得OC=2,
∴C(0,-2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(-2,3),
∴m=-2×3=-6,
∴y=
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,-2),
∴
,解得
,
∴y=
x-2;
(2)∵B(0,3),C(0,-2),
∴BC=5=OA,
在△OAC和△BCD中
∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如图,连接AD,
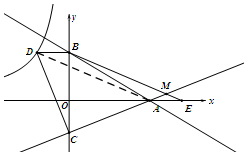
∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
(1)∵A(5,0),
∴OA=5.
∵tan∠OAC=
| 2 |
| 5 |
∴
| OC |
| OA |
| 2 |
| 5 |
∴C(0,-2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(-2,3),
∴m=-2×3=-6,
∴y=
| -6 |
| x |
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,-2),
∴
|
|
∴y=
| 2 |
| 5 |
(2)∵B(0,3),C(0,-2),
∴BC=5=OA,
在△OAC和△BCD中
|
∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如图,连接AD,

∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
看了 如图,已知点D在反比例函数y...的网友还看了以下:
设A={X/X^2+4X=0},B={X/X^2+2(a+1)X+a^2-1=0,a属于R}.(1 2020-04-06 …
已知椭圆T的方程为x^2/a^2+y^2/b^2=1(a>b>0),A(0,b),B(0,-b)和 2020-04-27 …
已知椭圆X^2/a^2+Y^2/b^2=1上任意一点M(除短轴端点外)与短轴两端点B1,B2的连线 2020-05-20 …
设A={x|x²+4x=0},B={x|x²+2(a+1)+a²-1=0}.(x²是x的平方,a² 2020-05-23 …
设A={x/x平方+4x=0},B={x/x平方+2(a+1)x+a平方-1=0}(1)若A交B= 2020-06-06 …
已知椭圆x^2/a^2+y^2/b^2=1(a>0,b>0),过点A(a,0)B(b,0)的直线倾 2020-06-23 …
沿x轴正方向运动的A质点和B质点,其位置-时间图象(如图所示)分别为图中直线a和曲线b,已知B质点 2020-07-31 …
成都七中的,两个二次项系数不相等的关于x的二次方程(a-1)x^2-(a^2+2)x+(a^2+2 2020-08-01 …
已知a>0,b>0且a+b=1,则(1/a^2-1)(1/b^2-1)的最小值是多少?(1/a²-1 2020-11-01 …
数轴上点A,B所代表的数为a,b,请你计算A,B两点的距离.a=2,b=6,A,B的距离是什么;a- 2020-12-30 …