P为双曲线x29-y216=1右支上一点，F1，F2分别为双曲线的左、右焦点，且PF1•PF2=0，直线PF2交y轴于点A，则△AF1P的内切圆半径为（）A.2B.3C.32D.132

Question

P为双曲线

(x2)/(9)-(y2)/(16)=1右支上一点，F₁，F₂分别为双曲线的左、右焦点，且

PF1

•

PF2

=0，直线PF₂交y轴于点A，则△AF₁P的内切圆半径为（　　）

A. 2

B. 3

C.

(3)/(2)

D.

(√(13))/(2)

Answer 1

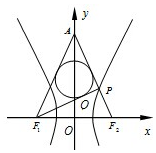根据题意，双曲线的方程(x2)/(9)-(y2)/(16)=1，其中a=√(9)=3，
设△APF₁的内切圆半径为r，∵PF₁⊥PF₂，
∴|PF₁|+|PA|-|AF₁|=2r，
∴|PF₂|+2a+|PA|-|AF₁|=2r，
∴|AF₂|-|AF₁|=2r-6，
∵由图形的对称性知：|AF₂|=|AF₁|，
即2r-6=0，解可得r=3，
故选：B．