已知双曲线-=1(a＞0b＞0)的左、右顶点分别为A、B，右焦点为F(c0)(c＞0)，右准线为l:x=|AF|=3.过点F作直线交双曲线的右支于P、Q两点，延长PB交右准线l于M点.(1)求双曲线的方程
- 
=1(a＞0 b＞0)的左、右顶点分别为A、B，右焦点为F(c 0)(c＞0)，右准线为l:x= 
|AF|=3.过点F作直线交双曲线的右支于P、Q两点，延长PB交右准线l于M点. (1)求双曲线的方程；
(2)若 
· 
=-17，求△PBQ的面积S.
- =1(a＞0 b＞0)的左、右顶点分别为A、B，右焦点为F(c 0)(c＞0)，右准线为l:x= |AF|=3.过点F作直线交双曲线的右支于P、Q两点，延长PB交右准线l于M点. (1)求双曲线的方程；
(2)若 · =-17，求△PBQ的面积S.
(1)求双曲线的方程；
(2)若 · =-17，求△PBQ的面积S.
(1)由题意知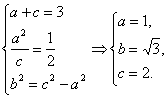
则双曲线方程为x 2 - =1.
(2)设P(x 1 y 1 )、Q(x 2 y 2 )，易得F(2 0)、A(-1 0)、B(1 0)，右准线l:x= 设PQ方程为y=k(x-2)
代入双曲线方程可得(3-k 2 )x 2 +4k 2 x-(4k 2 +3)=0.
由于P、Q都在双曲线的右支上，所以
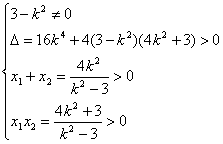
k 2 ＞3.
∴y 1 y 2 =k(x 1 -2)·k(x 2 -2)=k 2 ［x 1 x 2 -2(x 1 +x 2 )+4］= 
.
由于 
=(x 1 y 1 ) 
=(x 2 y 2 )
由 · =-17 可得x 1 x 2 +y 1 y 2 =-17 
- 
=-17 k 2 =4.
此时x 1 +x 2 =16 x 1 x 2 =19 y 1 y 2 =-36.
∴y 1 +y 2 =k(x 1 -2)+k(x 2 -2)
=k(x 1 +x 2 -4)
=12k.
∴S △ PBQ = |BF|×|y 1 -y 2 |
= ×1× 
= 
= 
=65.
(1)由题意知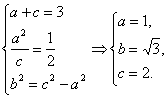
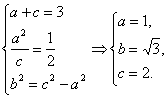
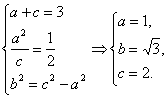
则双曲线方程为x 2 - =1.
=1. (2)设P(x 1 y 1 )、Q(x 2 y 2 )，易得F(2 0)、A(-1 0)、B(1 0)，右准线l:x= 设PQ方程为y=k(x-2)
设PQ方程为y=k(x-2) 代入双曲线方程可得(3-k 2 )x 2 +4k 2 x-(4k 2 +3)=0.
代入双曲线方程可得(3-k 2 2 )x 2 2 +4k 2 2 x-(4k 2 2 +3)=0.由于P、Q都在双曲线的右支上，所以
由于P、Q都在双曲线的右支上，所以 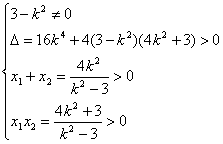k 2 ＞3.
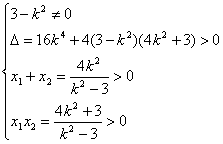
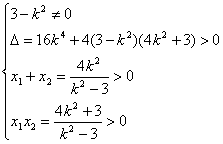
k 2 2 ＞3. ∴y 1 y 2 =k(x 1 -2)·k(x 2 -2)=k 2 ［x 1 x 2 -2(x 1 +x 2 )+4］= .
. 由于 =(x 1 y 1 ) =(x 2 y 2 )
=(x 1 1 y 1 1 ) =(x 2 2 y 2 2 ) 由 · =-17 可得x 1 x 2 +y 1 y 2 =-17 - =-17 k 2 =4.
· =-17 可得x 1 1 x 2 2 +y 1 1 y 2 2 =-17 - =-17 k 2 2 =4. 此时x 1 +x 2 =16 x 1 x 2 =19 y 1 y 2 =-36.
此时x 1 1 +x 2 2 =16 x 1 1 x 2 2 =19 y 1 1 y 2 2 =-36.∴y 1 +y 2 =k(x 1 -2)+k(x 2 -2)
∴y 1 1 +y 2 2 =k(x 1 1 -2)+k(x 2 2 -2)=k(x 1 +x 2 -4)
=k(x 1 1 +x 2 2 -4)=12k.
=12k. ∴S △ PBQ = |BF|×|y 1 -y 2 |
|BF|×|y 1 1 -y 2 2 | = ×1×
×1× =
=
=65.
=65.设双曲线C的中心在原点，以抛物线的顶点为双曲线的右焦点，抛物线的准线为双曲线的右准线．(1)试求双 2020-04-08 …
设双曲线C的中心在原点，以抛物线y2＝23x−4的顶点为双曲线的右焦点，抛物线的准线为双曲线的右准 2020-04-08 …
已知双曲线-=1(a＞0b＞0)的左、右顶点分别为A、B，右焦点为F(c0)(c＞0)，右准线为l 2020-04-08 …
已知双曲线x^2/a2-y^2/b^2=1(a>0,b>0)的左右两个顶点分别为A,B1,已知双曲 2020-05-17 …
p(x0,y0)(x0不=+-a)是双曲线E:x^2/a^2-y^2/b^2=1上一点,M,N分别 2020-07-26 …
过双曲线x^2/a^2-y^2/b^2=1的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线 2020-07-26 …
已知F为双曲线x2a2-y2b2=1（a>0，b>0）的右焦点，a为双曲线虚轴的一个顶点，过点F、 2020-07-30 …
是双曲线上一点，、分别是双曲线的左、右顶点，直线，的斜率之积为.(1)求双曲线的离心率；(2)过双 2020-08-01 …
已知是双曲线E:上的点，点MN分别是双曲线的左、右顶点，直线PMPN的斜率之积为。(1)求双曲线E的 2021-01-01 …
P（x，y）（x≠±a）是双曲线E：上一点，M，N分别是双曲线E的左右顶点，直线PM，PN的斜率之积 2021-01-23 …