早教吧作业答案频道 -->数学-->
在数列{an}中,如果对任意的n∈N*,都有(λ为常数),则称数列{an}为比等差数列,λ称为比公差.则下列命题中真命题的序号是①若数列{Fn}满足F1=1,F2=1,Fn=Fn-1+Fn
题目详情
在数列{a n }中,如果对任意的n∈N * ,都有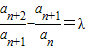 (λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是
(λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是
①若数列{F n }满足F 1 =1,F 2 =1,F n =F n-1 +F n-2 (n≥3),则该数列不是比等差数列;
②若数列{a n }满足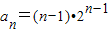 ,则数列{a n }是比等差数列,且比公差λ=2;
,则数列{a n }是比等差数列,且比公差λ=2;
③“等差数列是常数列”是“等差数列成为比等差数列”的充分必要条件;
④数列{a n }满足: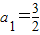 ,且
,且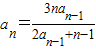 (n≥2,n∈N),则此数列的通项为
(n≥2,n∈N),则此数列的通项为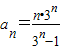 ,且{a n }不是比等差数列.
,且{a n }不是比等差数列.
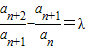 (λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是
(λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是 ①若数列{F n }满足F 1 =1,F 2 =1,F n =F n-1 +F n-2 (n≥3),则该数列不是比等差数列;
②若数列{a n }满足
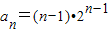 ,则数列{a n }是比等差数列,且比公差λ=2;
,则数列{a n }是比等差数列,且比公差λ=2;③“等差数列是常数列”是“等差数列成为比等差数列”的充分必要条件;
④数列{a n }满足:
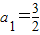 ,且
,且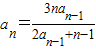 (n≥2,n∈N),则此数列的通项为
(n≥2,n∈N),则此数列的通项为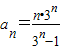 ,且{a n }不是比等差数列.
,且{a n }不是比等差数列. ▼优质解答
答案和解析
【答案】分析:根据比等差数列的定义(λ为常数),逐一判断①~④中的四个数列是否是比等差数列,即可得到答案.数列{Fn}满足F1=1,F2=1,F3=2,F4=3,F5=5,-=1,-=-≠1,则该数列不是比等差数列,故①正确;若数列{an}满足an=(n-1)•2n-1,则=不为定值,即数列{an}不是比等差数列,故②错误;等比数列=0,满足比等差数列的定义,若等差数列为an=n,则=不为定值,即数列{an}不是比等差数列,故③正确;数列{an}的通项公式为:,则,,,,=-,=-≠-,不满足比等差数列的定义,故④不正确;故答案为:①③点评:本题考查新定义,解题时应正确理解新定义,同时注意利用列举法判断命题为假,属于难题.
看了 在数列{an}中,如果对任意...的网友还看了以下:
命题r:如果则且;若命题r的否命题为p,命题r的否定为q,则A.P真q假B.P假q真C.p,q都真 2020-08-01 …
下列四句话中,正确的是()A.任何一个命题都有逆命题B.任何一个定理都有逆定理C.若原命题为真,则 2020-08-01 …
给出下列四个命题:①命题“若,则”的逆否命题为假命题;②命题:任意,都有,则“非”:存在,使;③“ 2020-08-01 …
举例说明一下.原命题为a,b都是偶数,则a+b是偶数,这是真的命题,否命题:a,b不都是偶数,则a 2020-08-01 …
已知原命题“菱形的对角线互相垂直”,则它的逆命题、否命题、逆否命题的真假判断正确的是()A.逆命题 2020-08-01 …
下列四句话中,正确的是()A.任何一个命题都有逆命题B.任何一个定理都有逆定理C.若原命题为真,则 2020-08-01 …
4、下列四句话中,正确的是()A、任何一个命题都有逆命题B、任何一个定理都有逆定理C、若原命题为真 2020-08-01 …
给出下列命题:①x2≠y2⇔x≠y或x≠-y;②命题“若a,b是偶数,则a+b是偶数”的逆否命题是 2020-08-01 …
下列判断正确的是()A.命题“a,b都是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a 2020-08-01 …
对于命题p和命题q,若p真q假,则命题p∧q和命题p∨q的真假为()A.p∧q和p∨q都为真B.p∧ 2020-12-13 …