早教吧作业答案频道 -->数学-->
(1)如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B>∠C,探究∠DAE与∠B,∠C的数量关系.(2)如图,F为AE上一点,FD⊥BC于D,则(1)中结论是否仍然成立?若成立说明理由;(3)当点F
题目详情
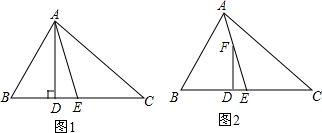
(1)如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B>∠C,探究∠DAE与∠B,∠C的数量关系.
(2)如图,F为AE上一点,FD⊥BC于D,则(1)中结论是否仍然成立?若成立说明理由;
(3)当点F在AE延长线上时,其余条件不变,则(1)中结论还能成立,画出图形并直接写出结论.
(2)如图,F为AE上一点,FD⊥BC于D,则(1)中结论是否仍然成立?若成立说明理由;
(3)当点F在AE延长线上时,其余条件不变,则(1)中结论还能成立,画出图形并直接写出结论.

▼优质解答
答案和解析
(1)∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
(180°-∠C-∠B),
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B,
∴∠EAD=∠BAE-∠BAD=
(180°-∠B-∠C)-(90°-∠B)=
∠B-
∠C;
(2)(1)中结论还能成立,如图2,过A作AM⊥BC于M,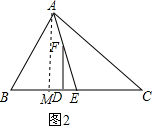
∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=
∠BAB=
(180°-∠B-∠C),
∵AM⊥BC,
∴∠AMC=90°,
∴∠BAM=90°-∠B,
∴∠EAM=∠BAE-∠BA=
(180°-∠C-∠B)-(90°-∠B)=
∠B-
∠C;
∵AM⊥BC,FD⊥BC,
∴AM∥FD,
∴∠EFD=∠EAM,
∴∠EFD=
∠B-
∠C;
(3)(1)中结论还能成立,如图3,
∵AE平分∠BAC,
∴∠CAE=
∠BAC.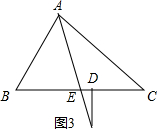
∵∠BAC=180°-(∠C+∠B);
∴∠CAE=
[180°-(∠C+∠B)];
∴∠FED=∠B+∠BAE=∠B+
[180°-(∠C+∠B)]=90°+
(∠C-∠B).
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+
(∠C-∠B)]=
(∠B-∠C).
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B,
∴∠EAD=∠BAE-∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)(1)中结论还能成立,如图2,过A作AM⊥BC于M,

∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AM⊥BC,
∴∠AMC=90°,
∴∠BAM=90°-∠B,
∴∠EAM=∠BAE-∠BA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AM⊥BC,FD⊥BC,
∴AM∥FD,
∴∠EFD=∠EAM,
∴∠EFD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)(1)中结论还能成立,如图3,
∵AE平分∠BAC,
∴∠CAE=
| 1 |
| 2 |

∵∠BAC=180°-(∠C+∠B);
∴∠CAE=
| 1 |
| 2 |
∴∠FED=∠B+∠BAE=∠B+
| 1 |
| 2 |
| 1 |
| 2 |
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+
| 1 |
| 2 |
| 1 |
| 2 |
看了(1)如图,△ABC中,AD是...的网友还看了以下:
英语翻译这是一只海豚.他得名字是***,他非常可爱.他来自海洋.他非常友好.(之类的,可以是当加点 2020-05-16 …
已知点P(2,0),Q(8,0),点M与点P的距离是它与点Q的距离的1/5,如何用几何画板探究点M 2020-05-21 …
如图,已知在△ABC中,AB=15,AC=20,cotA=2,P是边AB上的一个动点,⊙P的半径为 2020-06-13 …
关于besidesexcept的问题但是,当与nothing,nobody或noone等否定意义的 2020-06-17 …
丨a丨表示a与原点距离,当a=0时,丨a丨最小值为0;丨a-1丨表示a点与点1的距离,当a=1时, 2020-06-23 …
如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM 2020-06-23 …
如图,已知在△ABC中,AB=15,AC=20,tanA=12,点P在AB边上,P的半径为定长.当 2020-07-20 …
△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).(1)如图1,当点C与点 2020-07-26 …
在△ABC中,AC=BC,∠ACB=90°,D、E是直线AB上两点.∠DCE=45°(1)当CE⊥ 2020-07-27 …
O1与圆O2相交于点A,B,圆O1过圆O2,点C是圆O1的优弧AB上不与点A,B重合的动点,连接A 2020-07-31 …