设I为平面上以7x-5y-23=0x+7y-11=04x+y+10=0三直线所围成的三角形区域(包括三角形内部及边界)求P(xy)在平面I上变动时函数4x-3y的最大值和最小值.
设直线AB:7x-5y-23=0 AC:x+7y-11=0 BC:4x+y+10=0所围成的三角形为ABC
设t=4x-3y 则y=
x-
由于点(x y)在I上变动 因此当直线y= x- 过点B时 它在y轴上的截距- 为最小.
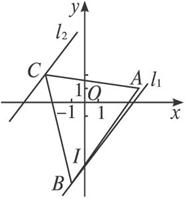
由
得B(-1 -6)
故(- ) min =-6+ =-
.所以t max =14.
当直线过点C时 直线y= x- 在y轴上的截距- 最大.
由
得C(-3 2).
故(
) max =2+4=6.所以t min =-18.
所以当P(x y)在I上变动时 函数4x-3y的最大值为14 最小值为-18.
求解线性代数设A是n阶矩阵，⑴若A满足矩阵方程A²-A+I=O，证明：A和I-A都可逆，并求解线性 2020-05-14 …
已知集合A={1234},函数fx的定义域,值域都是A,且对于任意i∈A,f（i）≠i．（求答疑） 2020-06-08 …
设f(z)=x^2+i*y^2,则f'(1+i)= 结果是2请问是怎么做的?另一个问题在复数范围内 2020-06-27 …
下列说法中正确的序号是①2+i>1+i②若一个数是实数，则其虚部不存在③虚轴上的点表示的数都是纯虚 2020-07-30 …
复变函数设曲线C是从0到1+(π/2)i的直线段，求积分∫cze^zdz学长，学姐求解答复变函数设曲 2020-11-04 …
已知集合A={1，2，3，4}，函数f（x）的定义域、值域都是A，且对于任意i∈A，f（i）≠i，设 2020-11-17 …
数学,线性代数,设A是方阵,A的k次方=0,k为正整数,求I+A+(A^2)/2!+(A^3)/.. 2020-11-20 …
在I/O设备、数据通道、时钟和软件这四项中，可能成为中断源的是。(A)I/O设备(B)I/O设备和数 2020-12-03 …
在I/O设备、数据通道、时钟和软件这四项中,可能成为中断源的是.(A)I/O设备(B)I/O设备和数 2020-12-03 …
函数与反函数...设函数f(x)在区间I内有定义连续单调减少且在I内具有连续的一阶二阶导数并在I内没 2021-01-23 …