早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,点E为AC上一点,且∠DEB=120°(1)求证:△ADE≌△ABE;(2)若∠DAB=60°,AD=23,求DE的长.
题目详情
如图,在菱形ABCD中,点E为AC上一点,且∠DEB=120°
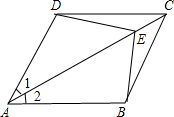
(1)求证:△ADE≌△ABE;
(2)若∠DAB=60°,AD=2
,求DE的长.

(1)求证:△ADE≌△ABE;
(2)若∠DAB=60°,AD=2
| 3 |
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是菱形,
∴AD=AB,∠1=∠2,
在△ADE和△ABE中
,
∴△ADE≌△ABE(SAS);
(2)∵△ADE≌△ABE,
∴∠1=∠2=
∠DAB=30°,
∠DEA=
∠DEB=60°,
∴∠ADE=90°,
在△DAE中,设DE=x,AE=2x,
由勾股定理得:AD2+DE2=AE2,
即(2
)2+x2=(2x)2,
解得:x=2,
∴DE=2.
∴AD=AB,∠1=∠2,
在△ADE和△ABE中
|
∴△ADE≌△ABE(SAS);
(2)∵△ADE≌△ABE,
∴∠1=∠2=
| 1 |
| 2 |
∠DEA=
| 1 |
| 2 |
∴∠ADE=90°,
在△DAE中,设DE=x,AE=2x,
由勾股定理得:AD2+DE2=AE2,
即(2
| 3 |
解得:x=2,
∴DE=2.
看了如图,在菱形ABCD中,点E为...的网友还看了以下:
已知函数f(x)的导数f′(x)=2x-9,且f(0)的值为整数,当x∈(n,n+1](n∈N*) 2020-05-13 …
已知数列的前n项和为,且,.(1)证明:是等比数列;(2)求数列的通项公式,并求出使得成立的最小正 2020-05-13 …
求下列双曲线的标准方程.(1)与椭圆x216+y225=1共焦点,且过点(1,52)的双曲线;(2 2020-05-13 …
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为 2020-06-20 …
齐次线性方程组λx1+x2+λ2x3=0x1+λx2+x3=0x1+x2+λx3=0的系数矩阵记为 2020-07-09 …
设a,b∈R,则“a>1且b>1”的充要条件是()A.a+b>2B.a+b>2且ab>1C.a+b 2020-07-12 …
(2014•大港区二模)已知数列{an}中,a1=1,a2=14,且an+1=(n−1)ann−a 2020-07-19 …
已知函数(a>0,且a≠1,k∈R).(1)若f(x)的图象关于直线y=x对称,且f(2)=-2l 2020-07-20 …
已知A,B是单位圆上的两点,O为圆心,且∠AOB=120°,MN是圆O的一条直径,点C在圆内,且满 2020-07-24 …
10.设奇函数f(x)在[-1,1]上是增函数,且f(-1)=一1.若函数,f(x)≤t2一2at+ 2020-11-07 …