早教吧作业答案频道 -->数学-->
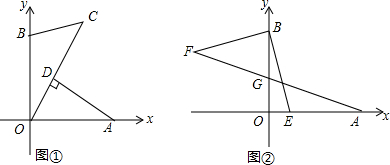
如图①,已知A(a,0),B(0,b),且a,b满足a2-8a+b2-8b=-32.(1)求A,B两点的坐标;(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;(3)如图②,若已知E(1
题目详情
如图①,已知A(a,0),B(0,b),且a,b满足a2-8a+b2-8b=-32.
(1)求A,B两点的坐标;
(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;
(3)如图②,若已知E(1,0),连接BE,过B作BF⊥BE且BF=BE,连接AF交y轴于G点,求G点的坐标.
(1)求A,B两点的坐标;
(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;
(3)如图②,若已知E(1,0),连接BE,过B作BF⊥BE且BF=BE,连接AF交y轴于G点,求G点的坐标.

▼优质解答
答案和解析
(1) ∵a2-8a+b2-8b=-32,
∴(a2-8a+16)+(b2-8b+16)=0,
∴(a-4)2+(b-4)2=0,
∵(a-4)2≥0,(b-4)2≥0,
∴a=b=4,
∴点A坐标为(4,0),点B坐标为(0,4).
(2)证明:∵点A坐标为(4,0),点B坐标为(0,4),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°,
∴∠BCO=∠BAO,
∴O、A、C、B四点共圆,
∴∠AOB+∠BCA=180°,
∵∠AOB=90°,
∴∠BCA=90°,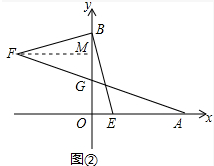
∴∠DCA=90°-∠BCA=45°,
∵AD⊥CD,
∴∠ADC=90°,∠DCA=∠DAC=45°,
∴DC=DA.
(3) 作FM⊥OB于M,
∵∠FBM+∠OBE=90°,∠OBE+∠OEB=90°,
∴∠FBM=∠BEO,
在△FBM和△BEO中,
,
∴△BFM≌△EBO,
∴FM=BO=AO,BM=OE=1,OM=3,
∵FM∥AO,
∴∠FMG=∠AOG,
在△FMG和△AOG中,
,
∴△FMG≌△AOG,
∴MG=OG=
OM=
,
∴点M坐标(0,
).

∴(a2-8a+16)+(b2-8b+16)=0,
∴(a-4)2+(b-4)2=0,
∵(a-4)2≥0,(b-4)2≥0,
∴a=b=4,
∴点A坐标为(4,0),点B坐标为(0,4).
(2)证明:∵点A坐标为(4,0),点B坐标为(0,4),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°,
∴∠BCO=∠BAO,
∴O、A、C、B四点共圆,
∴∠AOB+∠BCA=180°,
∵∠AOB=90°,
∴∠BCA=90°,

∴∠DCA=90°-∠BCA=45°,
∵AD⊥CD,
∴∠ADC=90°,∠DCA=∠DAC=45°,
∴DC=DA.
(3) 作FM⊥OB于M,
∵∠FBM+∠OBE=90°,∠OBE+∠OEB=90°,
∴∠FBM=∠BEO,
在△FBM和△BEO中,
|
∴△BFM≌△EBO,
∴FM=BO=AO,BM=OE=1,OM=3,
∵FM∥AO,
∴∠FMG=∠AOG,
在△FMG和△AOG中,
|
∴△FMG≌△AOG,
∴MG=OG=
| 1 |
| 2 |
| 3 |
| 2 |
∴点M坐标(0,
| 3 |
| 2 |
看了如图①,已知A(a,0),B(...的网友还看了以下:
平面直角坐标系中,A(4,8)、C(0,6),过A点作AB⊥x轴于B,平面直角坐标系中,A(4,8 2020-05-15 …
已知在椭圆E:x的平方/a的平方+y的平方/b的平方=1(a>b>0)中,以F1(-C,0)为圆心 2020-05-22 …
如图点F1(-c,0)F2(c,0)分别是椭圆C(a>b>0)的左右焦点,点F1(-c,0)F2 2020-06-21 …
无机化学作业,请教据能斯特方程式,计算298K时下列电极的点位(1)Cu2+(c=0.01mol/ 2020-07-19 …
求系统在单位阶跃输入作用下的输出响应已知单位负反馈系统的开环传递函数为G(s)=2/S(S+3); 2020-07-30 …
解指数方程!0.8^x-C*0.6^x=1-C,其中C为常数.0.8**x-C*(0.6**x)= 2020-08-01 …
在平面直角坐标系xoy中,过定点c(0,p)作直线与抛物线y^2=2py(p>0)交于a,b两点, 2020-08-02 …
已知向量a=(1,1),b=(1,0),向量c满足a*c=0,且a的模=c的模,b*c>0若将(x, 2020-12-09 …
这是哪的中考题?如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.如图,抛物线经过A( 2020-12-12 …
多元一次方程求解a=0.1072(a+b+c+d+e)b=0.041(a+b+c+d+e)c=0.2 2020-12-14 …