早教吧作业答案频道 -->数学-->
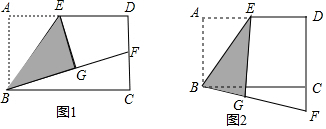
在长方形ABCD中,点E是AD的中点,将△ABE沿BE折叠后得到对应的△GBE,BG延长交DC于点F.(1)如果点G在长方形ABCD的内部,如图1所示.①求证:GF=DF;②若DF=12DC,AD=4,求AB的长度.(2)如果点
题目详情
在长方形ABCD中,点E是AD的中点,将△ABE沿BE折叠后得到对应的△GBE,BG延长交DC于点F.
(1)如果点G在长方形ABCD的内部,如图1所示.
①求证:GF=DF;
②若DF=
DC,AD=4,求AB的长度.
(2)如果点G在长方形ABCD的外部,如图2所示,DF=kDC(k>1),请用含k的代数式表示
的值.
(1)如果点G在长方形ABCD的内部,如图1所示.
①求证:GF=DF;
②若DF=
| 1 |
| 2 |
(2)如果点G在长方形ABCD的外部,如图2所示,DF=kDC(k>1),请用含k的代数式表示
| AD |
| AB |

▼优质解答
答案和解析
(1)①证明:如图1中,连接EF.
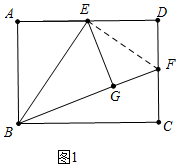
∵矩形ABCD中,E是AD的中点,△ABE沿BE折叠后得到△GBE,
∴AE=DE,AE=EG,∠A=∠BGE=∠D=90°,
在Rt△EFG和Rt△EFG中,
,
∴Rt△EGF≌Rt△EDF,
∴FG=DF;
②设DF=FC=a,则AB=BG=2a,GF=a,
在Rt△BFC中,∵BF2=CF2+BC2,
∴(3a)2+a2=42,
解得a=
,
∴AB=2a=
.
(2)如图2中,连接EF.
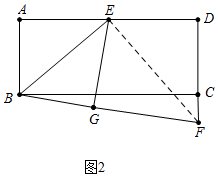
由(1)可知,△EFG≌△EFD,
∴∠FED=∠FEG,FD=FG,∵∠BEA=∠BEG,
∴∠BEF=90°,
∵∠BEG+∠FEG=90°,∠FEG+∠EFG=90°,
∠BEG=∠EFG,∵∠BGE=∠FGE=90°,
∴△BEG∽△EFG,
∴
=
,
∴EG2=BG•GF,设DC=AB=BG=a,则DF=FG=ka,
∴EG2=ka2,
∴EG=
a,
∴AD=2EG=2
a,
∴
=
=2
.

∵矩形ABCD中,E是AD的中点,△ABE沿BE折叠后得到△GBE,
∴AE=DE,AE=EG,∠A=∠BGE=∠D=90°,
在Rt△EFG和Rt△EFG中,
|
∴Rt△EGF≌Rt△EDF,
∴FG=DF;
②设DF=FC=a,则AB=BG=2a,GF=a,
在Rt△BFC中,∵BF2=CF2+BC2,
∴(3a)2+a2=42,
解得a=
2
| ||
| 5 |
∴AB=2a=
4
| ||
| 5 |
(2)如图2中,连接EF.

由(1)可知,△EFG≌△EFD,
∴∠FED=∠FEG,FD=FG,∵∠BEA=∠BEG,
∴∠BEF=90°,
∵∠BEG+∠FEG=90°,∠FEG+∠EFG=90°,
∠BEG=∠EFG,∵∠BGE=∠FGE=90°,
∴△BEG∽△EFG,
∴
| EG |
| FG |
| BG |
| EG |
∴EG2=BG•GF,设DC=AB=BG=a,则DF=FG=ka,
∴EG2=ka2,
∴EG=
| k |
∴AD=2EG=2
| k |
∴
| AD |
| AB |
2
| ||
| a |
| k |
看了在长方形ABCD中,点E是AD...的网友还看了以下:
正方体中证明三点共线,在正方体ABCD-A'B'C'D'中,点E、F分别是AA’、CC’的中点,连结 2020-03-30 …
定积分中值定理的证明中,证明在[a,b]内至少存在一点s.这里证明的时候直接用了连续函数介值定理, 2020-06-03 …
几何题 无图 自己构思图形1在正方形ABCD中作一点M,证明三角形ABM,BCM,CDM,DAM的 2020-06-27 …
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的 2020-07-27 …
如图,AB是⊙O的直径,过圆上一点D作⊙O的切线DE,与过点A的直线垂直于E,弦BD的延长线与直线 2020-07-31 …
如图,在平行四边形ABCD中,AC,BD相交于点O,OE∥AB,交BC于点E,连接DE,交OC于点 2020-08-02 …
如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两 2020-08-03 …
已知:在正方形ABCD中,点E、F分别是CB、CD延长线上的点,且BE=DF,联结AE、AF、DE、 2020-10-31 …
(2014•汕尾)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点 2020-11-12 …
(2014•江都区模拟)如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长 2020-12-14 …