早教吧作业答案频道 -->数学-->
已知:在正方形ABCD中,点E、F分别是CB、CD延长线上的点,且BE=DF,联结AE、AF、DE、DE交AB于点M.(1)如图1,当E、A、F在一直线上时,求证:点M为ED中点;(2)如图2,当AF∥ED,求证:AM2=AB•
题目详情
已知:在正方形ABCD中,点E、F分别是CB、CD延长线上的点,且BE=DF,联结AE、AF、DE、DE交AB于点M.
(1)如图1,当E、A、F在一直线上时,求证:点M为ED中点;
(2)如图2,当AF∥ED,求证:AM2=AB•BM.
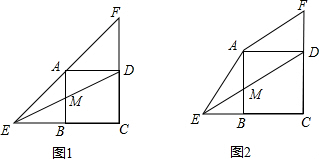
(1)如图1,当E、A、F在一直线上时,求证:点M为ED中点;
(2)如图2,当AF∥ED,求证:AM2=AB•BM.

▼优质解答
答案和解析
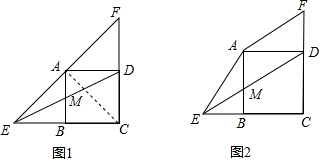 (1)连接AC,∵四边形ABCD是正方形,
(1)连接AC,∵四边形ABCD是正方形,
∴∠DAM=∠BEM=∠BCD=90°,∠BCA=∠DCA=45°,AB=BC=CD=DA,
∵BE=DF,∴CE=CF,
∴∠AEB=∠F=45°,
∴BE=BA=AD,
在△ADM和△BEM中,
,
∴△ADM和△BEM,
∴DM=EM,即点M为ED中点;
(2) ∵四边形ABCD是正方形,
∴∠DAM=∠EBM=90°,AD=AB,
∴△ADM∽△BEM,
∴
=
,
∵AM∥DF,AF∥DE,
∴四边形AMDF是平行四边形,
∴AM=DF,
∵BE=DF,
∴AM=BE,
∴
=
,
∴AM2=AB•BM.
 (1)连接AC,∵四边形ABCD是正方形,
(1)连接AC,∵四边形ABCD是正方形,∴∠DAM=∠BEM=∠BCD=90°,∠BCA=∠DCA=45°,AB=BC=CD=DA,
∵BE=DF,∴CE=CF,
∴∠AEB=∠F=45°,
∴BE=BA=AD,
在△ADM和△BEM中,
|
∴△ADM和△BEM,
∴DM=EM,即点M为ED中点;
(2) ∵四边形ABCD是正方形,
∴∠DAM=∠EBM=90°,AD=AB,
∴△ADM∽△BEM,
∴
| AM |
| BM |
| AD |
| BE |
∵AM∥DF,AF∥DE,
∴四边形AMDF是平行四边形,
∴AM=DF,
∵BE=DF,
∴AM=BE,
∴
| AM |
| BM |
| AB |
| AM |
∴AM2=AB•BM.
看了已知:在正方形ABCD中,点E...的网友还看了以下:
一道锐角三角比的题!正方形ABCD中,点E、F分别在边CD、AD上,且EF=3,BE=4,BF=5 2020-04-27 …
如图,已知在平行四边形ABCD中, DE垂直AB于E,DF垂直于BC,角DAB的平分线AP交DE于 2020-05-16 …
如图,在△ABC中,以AB为直径作⊙O交BC于点D,DE交AC于E.(1)若AB=AC,DE⊥AC 2020-05-16 …
已知,如图,AB为圆O的直径,圆O过AC的中点D,DE垂直BC于点E.《1》求证:DE为圆O的切线 2020-05-16 …
中考变试题.如图,在菱形abcd中,对角线ac,bd交于o,与ob为直径画圆m如图,在菱形abcd 2020-06-23 …
如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM 2020-06-23 …
以△ABC的两边AB、AC为腰分别向外作等腰Rt△ABD和等腰Rt△ACE,∠BAD=∠CAE=9 2020-07-17 …
在三角形ABC中,AB=AC,AD垂直BC于D,DE垂直AC于E,M为DE中点,AM与BE相交于N 2020-07-22 …
如图,在三角形ABC中,AB=AC,AD垂直于BC于D,DE垂直于AC于E,M为DE的中点,求证A 2020-07-22 …
如图,在△ABC中,矩形DEFG,G、F在BC上,D、E分别在AB、AC上,AH⊥BC交DE于M, 2020-07-27 …