早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.(1)求证:点E是AB的中点;(2)求证:四边形ACEF是平行四边形.
题目详情
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.
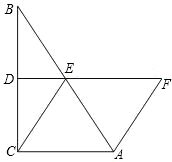
(1)求证:点E是AB的中点;
(2)求证:四边形ACEF是平行四边形.

(1)求证:点E是AB的中点;
(2)求证:四边形ACEF是平行四边形.
▼优质解答
答案和解析
(1)证明:∵∠ACB=90°,DE是BC的中垂线,
∴DE⊥BC,
又∵AC⊥BC,
∴DE∥AC,
又∵D为BC中点,DF∥AC,
∴DE是△ABC的中位线,
∴E为AB边的中点;
(2)证明:∵E为AB边的中点,
∴CE=AE=BE,
∵AF=CE,
∴CE=AE=AF,
∴∠ECA=∠EAC,∠AEF=∠F,
∵DE∥AC,
∴∠EAC=∠AEF,∠FEC+∠ECA=180°,
∴∠ECA=∠F,
∴∠FEC+∠F=180°,
∴AF∥CE,
∴四边形ACEF是平行四边形.
∴DE⊥BC,
又∵AC⊥BC,
∴DE∥AC,
又∵D为BC中点,DF∥AC,
∴DE是△ABC的中位线,
∴E为AB边的中点;
(2)证明:∵E为AB边的中点,
∴CE=AE=BE,
∵AF=CE,
∴CE=AE=AF,
∴∠ECA=∠EAC,∠AEF=∠F,
∵DE∥AC,
∴∠EAC=∠AEF,∠FEC+∠ECA=180°,
∴∠ECA=∠F,
∴∠FEC+∠F=180°,
∴AF∥CE,
∴四边形ACEF是平行四边形.
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
按要求填空:(1)以下列出的是一些原子的2p能级和3d能级中电子排布的情况.试判断,违反了泡利原理 2020-05-13 …
下面现象中是平移的有,是旋转的有.A.狗拉雪橇B.升国旗C.拧开瓶盖D.单摆运动E.拉出抽屉F.转 2020-05-13 …
结合如图图示回答问题(1)在A、B、C、D四个结构示意图中,属于同种元素的是;微粒C的符号是.(2 2020-05-13 …
下列现象中属于机械运动的是.a.五四运动b.开水变凉c.铁生锈了d.一行白鸳上青天e.大地震f.霜 2020-07-03 …
下列变化属于物理变化的是(填字母,下同),属于化学变化的是.A.樟脑丸消失B.蜡烛燃烧C.铁生锈D 2020-07-05 …
某课题组以甲苯为主要原料,采用以下路线合成7-氨基异喹啉:已知:.请回答下列问题:(1)对于化合物E 2020-10-31 …
矩阵的选择题单项选择:单项选择题已知A为n阶方阵,E为n阶单位阵,且(A-E)^2=3(A+E)^2 2020-11-03 …
(2006•潍坊)读我国某地区地形图,完成下列各题:(1)关于图中的地形类型,正确的是.A.A处是山 2020-11-13 …
下列变化中,属于物理变化的有,属于化学变化的有.A.电灯发亮B.镁条燃烧C.酒精燃烧D.白糖受热变成 2020-12-07 …
下列变化中,属于物理变化的有,属于化学变化的有.A.电灯发亮B.镁条燃烧C.酒精燃烧D.白糖受热变成 2020-12-07 …