早教吧作业答案频道 -->数学-->
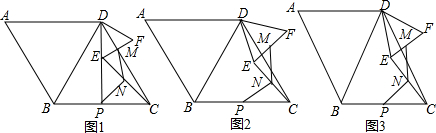
在菱形ABCD中,∠A=60°,以D为顶点作等边三角形DEF,连接EC,点N、P分别为EC、BC的中点,连接NP(1)如图1,若点E在DP上,EF与CD交于点M,连接MN,CE=3,求MN的长;(2)如图2,若M为EF中点,求
题目详情
在菱形ABCD中,∠A=60°,以D为顶点作等边三角形DEF,连接EC,点N、P分别为EC、BC的中点,连接NP
(1)如图1,若点E在DP上,EF与CD交于点M,连接MN,CE=3,求MN的长;
(2)如图2,若M为EF中点,求证:MN=PN;
(3)如图3,若四边形ABCD为平行四边形,且∠A=∠DBC≠60°,以D为顶点作三角形DEF,满足DE=DF且∠EDF=∠ABD,M、N、P仍分别为EF、EC、BC的中点,请探究∠ABD与∠MNP的和是否为一个定值,并证明你的结论.
(1)如图1,若点E在DP上,EF与CD交于点M,连接MN,CE=3,求MN的长;
(2)如图2,若M为EF中点,求证:MN=PN;
(3)如图3,若四边形ABCD为平行四边形,且∠A=∠DBC≠60°,以D为顶点作三角形DEF,满足DE=DF且∠EDF=∠ABD,M、N、P仍分别为EF、EC、BC的中点,请探究∠ABD与∠MNP的和是否为一个定值,并证明你的结论.

▼优质解答
答案和解析
(1)如图1,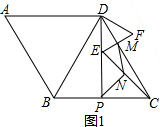 ,
,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
又∵∠A=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,
∴BC=CD=BD,
∴△BCD是等边三角形,
又∵P为BC的中点,
∴DP是∠BDC的平分线,
∴∠CDP=60°÷2=30°,
又∵三角形DEF是等边三角形,
∴∠DEF=60°,
∴∠DME=180°-30°-60°=90°,
在Rt△CME中,
∵N为EC的中点,
∴MN=
CE=
×3=
,
即MN的长是
.
(2)如图2,连接BE、CF,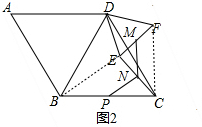 ,
,
∵点N、M分别为EC、EF的中点,
∴MN是△CEF的中位线,
∴MN=
CF;
∵点N、P分别为EC、BC的中点,
∴PN是△CBE的中位线,
∴PN=
BE;
∵∠BDC=60°,∠EDF=60°,
∴∠BDC-∠EDC=∠EDF-∠EDC,
即∠BDE=∠CDF,
在△BDE和△∠CDF中,
∴△BDE≌△∠CDF,
∴CF=BE,
∴MN=PN.
(3)∠ABD与∠MNP的和是一个定值,∠ABD+∠MNP=180°.
证明:如图3,连接BE、CF,延长CE交BD于点G,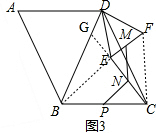 ,
,
∵点N、M分别为EC、EF的中点,
∴MN是△CEF的中位线,
∴MN∥CF,
∴∠MNE=∠FCE=∠FCD+∠DCE,
∵点N、P分别为EC、BC的中点,
∴PN是△CBE的中位线,
∴PN∥BE,
∴∠ENP=∠BEG,
∵AB∥CD,
∴∠BDC=∠ABD,
又∵∠EDF=∠ABD,
∴∠BDC=∠EDF,
∴∠BDC-∠EDC=∠EDF-∠EDC,
即∠BDE=∠CDF,
∵∠A=∠DBC,∠ADB=∠DBC,
∴∠A=∠ADB,
∴AB=BD,
又∵AB=CD,
∴BD=CD,
在△BDE和△∠CDF中,
∴△BDE≌△∠CDF,
∴∠DBE=∠DCF,
根据三角形的外角的性质,可得
∠BGE=∠BDC+∠DCE,
在△BGE中,
∠BEG+∠BGE+∠GBE=180°,
∴∠ENP+(∠BDC+∠DCE)+∠DCF=180°,
∴(∠ENP+∠DCF+∠DCE)+∠BDC=180°,
又∵∠ENP+∠DCF+∠DCE=∠MNP,∠BDC=∠ABD,
∴∠ABD+∠MNP=180°,
即∠ABD与∠MNP的和是一个定值.
 ,
,∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
又∵∠A=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,
∴BC=CD=BD,
∴△BCD是等边三角形,
又∵P为BC的中点,
∴DP是∠BDC的平分线,
∴∠CDP=60°÷2=30°,
又∵三角形DEF是等边三角形,
∴∠DEF=60°,
∴∠DME=180°-30°-60°=90°,
在Rt△CME中,
∵N为EC的中点,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即MN的长是
| 3 |
| 2 |
(2)如图2,连接BE、CF,
 ,
,∵点N、M分别为EC、EF的中点,
∴MN是△CEF的中位线,
∴MN=
| 1 |
| 2 |
∵点N、P分别为EC、BC的中点,
∴PN是△CBE的中位线,
∴PN=
| 1 |
| 2 |
∵∠BDC=60°,∠EDF=60°,
∴∠BDC-∠EDC=∠EDF-∠EDC,
即∠BDE=∠CDF,
在△BDE和△∠CDF中,
|
∴△BDE≌△∠CDF,
∴CF=BE,
∴MN=PN.
(3)∠ABD与∠MNP的和是一个定值,∠ABD+∠MNP=180°.
证明:如图3,连接BE、CF,延长CE交BD于点G,
 ,
,∵点N、M分别为EC、EF的中点,
∴MN是△CEF的中位线,
∴MN∥CF,
∴∠MNE=∠FCE=∠FCD+∠DCE,
∵点N、P分别为EC、BC的中点,
∴PN是△CBE的中位线,
∴PN∥BE,
∴∠ENP=∠BEG,
∵AB∥CD,
∴∠BDC=∠ABD,
又∵∠EDF=∠ABD,
∴∠BDC=∠EDF,
∴∠BDC-∠EDC=∠EDF-∠EDC,
即∠BDE=∠CDF,
∵∠A=∠DBC,∠ADB=∠DBC,
∴∠A=∠ADB,
∴AB=BD,
又∵AB=CD,
∴BD=CD,
在△BDE和△∠CDF中,
|
∴△BDE≌△∠CDF,
∴∠DBE=∠DCF,
根据三角形的外角的性质,可得
∠BGE=∠BDC+∠DCE,
在△BGE中,
∠BEG+∠BGE+∠GBE=180°,
∴∠ENP+(∠BDC+∠DCE)+∠DCF=180°,
∴(∠ENP+∠DCF+∠DCE)+∠BDC=180°,
又∵∠ENP+∠DCF+∠DCE=∠MNP,∠BDC=∠ABD,
∴∠ABD+∠MNP=180°,
即∠ABD与∠MNP的和是一个定值.
看了在菱形ABCD中,∠A=60°...的网友还看了以下:
连续极限{[(1+x)(1/x次方)]/e}(1/x次方)求X->0极限书上说是e(-1/2次方) 2020-04-27 …
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=( )如 2020-05-13 …
讨论fx=1/(1+e^1/x)x≠0在点x=0处的左右连续性讨论f(x)=1/(1+e^1/x) 2020-06-10 …
如图,在三角形ABC中,角C等于2角B,D是BC上的一点,且AD垂直AB,点E是BD的中点,连接E 2020-06-27 …
如图,在△ABC中,∠ACB=90°,∠A=60°,AC=3,点D是边AB上的动点(点D与点A、B 2020-07-20 …
如图,已知矩形ABCD满足AB:BC=1:2,把矩形ABCD对折,使CD与AB重合,得折痕EF,把 2020-07-21 …
f(x)=1/π*arctan(1/x)+(a+be^(1/x))/(1+e^(1/x))(x≠0 2020-07-22 …
求解f(x)在x=0处是否连续和一题极限f(x)=e^(-1/x^2)x0=0x=0二段函数,答案书 2020-11-01 …
在矩形ABCD中,AB=2,CD=3,是BC上的任意一点[P与B.C不重合,过点P作AP垂直PE,垂 2021-01-11 …
设f(x)在(0,1)连续,在(0,1)内可导,证明:存在x属于(0,1),使得f(x)+fx的导数 2021-01-13 …