早教吧作业答案频道 -->数学-->
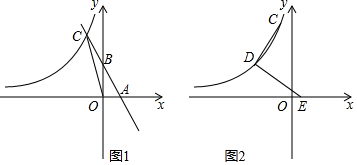
如图1,直线y=-2x+4交x轴、y轴于A、B两点,交双曲线y=kx(x<0)于C点,△AOC的面积为6.(1)求双曲线的解析式.(2)如图2,D为双曲线y=kx(x<0)上一点,连结CD,将线段CD绕点D顺时针旋转
题目详情
如图1,直线y=-2x+4交x轴、y轴于A、B两点,交双曲线y=
(x<0)于C点,△AOC的面积为6.
(1)求双曲线的解析式.
(2)如图2,D为双曲线y=
(x<0)上一点,连结CD,将线段CD绕点D顺时针旋转90°得线段DE,点E恰好落在x轴上,求点E的坐标.
| k |
| x |
(1)求双曲线的解析式.
(2)如图2,D为双曲线y=
| k |
| x |

▼优质解答
答案和解析
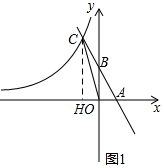 (1)过C作CH⊥x轴于H,
(1)过C作CH⊥x轴于H,
直线y=-2x+4中,令y=0,则x=2,
∴A(2,0),即AO=2,
∵△AOC的面积为6,
∴
×AO×CH=6,
∴
×2×CH=6,
∴CH=6,即点C的纵坐标为6,
直线y=-2x+4中,当y=6时,6=-2x+4,
解得x=-1,
∴C(-1,6),
代入y=
(x<0)可得,k=-1×6=-6,
∴双曲线的解析式为y=-
;
(2)过点D作DF⊥x轴于F,过C作CG⊥DF于G,则∠G=∠DFE=90°,
由旋转可得,CD=DE,∠CDE=90°,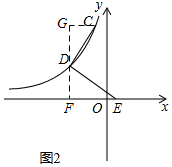
∴∠CDG=∠DEF,
在△DCG和△EDF中,
,
∴△DCG≌△EDF(AAS),
∴CG=DF,DG=EF,
设D(a,-
),则DF=-
,FO=-a,
∵C(-1,6),
∴CG=-1-a,
∴DF=-1-a,
∴-
=-1-a,
解得a=-3或a=2(舍去),
∴DF=-1+3=2,DG=GF-DF=6-2=4,
∴EF=4,
又∵FO=3,
∴OE=4-3=1,
∴E(1,0).
 (1)过C作CH⊥x轴于H,
(1)过C作CH⊥x轴于H,直线y=-2x+4中,令y=0,则x=2,
∴A(2,0),即AO=2,
∵△AOC的面积为6,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴CH=6,即点C的纵坐标为6,
直线y=-2x+4中,当y=6时,6=-2x+4,
解得x=-1,
∴C(-1,6),
代入y=
| k |
| x |
∴双曲线的解析式为y=-
| 6 |
| x |
(2)过点D作DF⊥x轴于F,过C作CG⊥DF于G,则∠G=∠DFE=90°,
由旋转可得,CD=DE,∠CDE=90°,

∴∠CDG=∠DEF,
在△DCG和△EDF中,
|
∴△DCG≌△EDF(AAS),
∴CG=DF,DG=EF,
设D(a,-
| 6 |
| a |
| 6 |
| a |
∵C(-1,6),
∴CG=-1-a,
∴DF=-1-a,
∴-
| 6 |
| a |
解得a=-3或a=2(舍去),
∴DF=-1+3=2,DG=GF-DF=6-2=4,
∴EF=4,
又∵FO=3,
∴OE=4-3=1,
∴E(1,0).
看了如图1,直线y=-2x+4交x...的网友还看了以下:
已知函数f(x)=x^3+x-16.直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切 2020-05-20 …
在同一坐标系中,将曲线y=3sin2x变为曲线y′=sinx′的伸缩变换是()A.x=2x′y=1 2020-07-13 …
帮忙解决下这几道关于导数德题目.已知直线L为曲线y=Xˇ2+X+2在点(1,0)处的切线,K为该曲 2020-07-30 …
直线与曲线相切不一定只有一个公共点那如何证明相切已知直线L1为曲线y=x^2+x-2在点(1,0) 2020-07-30 …
三题积分题1已知曲线y=x^3+ax^2-9x+4在x=1有拐点,试确定系数a,并求曲线的拐点坐标 2020-07-31 …
三题积分题1已知曲线y=x^3+ax^2-9x+4在x=1有拐点,试确定系数a,并求曲线的拐点坐标 2020-07-31 …
已知l:y=kx+b为曲线y=f(x)的“渐近线”,给出定义域均为D={x|x>1}的函数如下:① 2020-08-01 …
已知函数f(x)=ex-12x2,设l为曲线y=f(x)在点P(x0,f(x0))处的切线,其中x0 2020-10-31 …
设曲面S为曲线y=(1+z^2)^1/2,x=0(1≤z≤2)绕z轴旋转一周而形成的曲面,其法向量与 2020-11-01 …
已知P为曲线y=x三次方上一点,P点的横坐标为1则该曲线在点P处的切线方程y=x³y'=3x²点P处 2021-02-03 …