已知正方形ABCD，AB=8，点E、F分别从点A、D同时出发，以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动，设运动时间为t．（1）求证：OE=OF．（2）在点E、F的运动过程中，连结AF．设线段A

Question

已知正方形ABCD，AB=8，点E、F分别从点A、D同时出发，以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动，设运动时间为t．

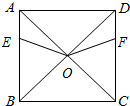
（1）求证：OE=OF．
（2）在点E、F的运动过程中，连结AF．设线段AE、OE、OF、AF所形成的图形面积为S．
探究：①S的大小是否会随着运动时间为t的变化而变化？若会变化，试求出S与t的函数关系式；若不会变化，请说明理由．
②连结EF，当运动时间为t为何值时，△OEF的面积恰好等于的(1)/(3)S．

Answer 1

（1）证明：∵四边形ABCD是正方形，
∴OA=OD，∠EAO=∠FDO=45°，
∵点E、F分别从点A、D同时出发，以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动，设运动时间为t，
∴AE=DF=t，
在△EAO和△FDO中

OA=OD

∠EAO=∠FDO

AE=DF

∴△EAO≌△FDO（SAS），
∴OE=OF；

（2） ①S的大小不会随着运动时间为t的变化而变化，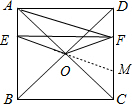
理由是：延长EO交DC于M，
∵四边形ABCD是正方形，
∴∠OAE=∠MCO=45°，OA=OC，
在△AOE和△COM中

∠EAO=∠MCO

AO=CO

∠AOE=∠COM

∴△AOE≌△COM（ASA），
∴AE=CM=t，
∴S=S_{四边形AEMF}-S_△FOM
=(1)/(2)（t+8-t-t）•8-(1)/(2)×（8-t-t）•4
=16，
所以S的大小不会随着运动时间为t的变化而变化；

②∵△AOE≌△COM，
∴OE=OM，
∴S_△EOF=S_△FOM=(1)/(2)S_△EFM=(1)/(2)×(1)/(2)（8-t-t）•8=16-4t，
∵△OEF的面积恰好等于的(1)/(3)S，
∴16-4t=(1)/(3)×16，
解得：t=(8)/(3)，
即当运动时间为t为(8)/(3)时，△OEF的面积恰好等于的(1)/(3)S．