早教吧作业答案频道 -->数学-->
设函数f(x)=lnx+mx,m∈R(1)当m=e(e为自然对数的底数)时,f(x)的极小值;(2)若函数g(x)=f′(x)-x3存在唯一零点,求m的范围.
题目详情
设函数f(x)=lnx+
,m∈R
(1)当m=e(e为自然对数的底数)时,f(x)的极小值;
(2)若函数g(x)=f′(x)-
存在唯一零点,求m的范围.
| m |
| x |
(1)当m=e(e为自然对数的底数)时,f(x)的极小值;
(2)若函数g(x)=f′(x)-
| x |
| 3 |
▼优质解答
答案和解析
解 (1)由题设,当m=e时,f(x)=ln x+
,
则f′(x)=
,由f′(x)=0,得x=e.
∴当x∈(0,e),f′(x)<0,f(x)在(0,e)上单调递减,
当x∈(e,+∞),f′(x)>0,f(x)在(e,+∞)上单调递增,
∴当x=e时,f(x)取得极小值f(e)=ln e+
=2,
∴f(x)的极小值为2…(4分)
(2)由题设g(x)=f′(x)-
=
-
-
(x>0),
令g(x)=0,得m=-
x3+x(x>0).
设φ(x)=-
x3+x(x≥0),
则φ′=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
∴x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是φ(x)的最大值点.
∴φ(x)的最大值为φ(1)=
.
又φ(0)=0,结合y=φ(x)的图象(如图),
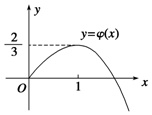
可知
当m=
时,函数g(x)有且只有一个零点;
当m≤0时,函数g(x)有且只有一个零点.
所以,当m=
或m≤0时,函数g(x)有且只有一个零点;…(12分)
| e |
| x |
则f′(x)=
| x-e |
| x2 |
∴当x∈(0,e),f′(x)<0,f(x)在(0,e)上单调递减,
当x∈(e,+∞),f′(x)>0,f(x)在(e,+∞)上单调递增,
∴当x=e时,f(x)取得极小值f(e)=ln e+
| e |
| e |
∴f(x)的极小值为2…(4分)
(2)由题设g(x)=f′(x)-
| x |
| 3 |
| 1 |
| x |
| m |
| x2 |
| x |
| 3 |
令g(x)=0,得m=-
| 1 |
| 3 |
设φ(x)=-
| 1 |
| 3 |
则φ′=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
∴x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是φ(x)的最大值点.
∴φ(x)的最大值为φ(1)=
| 2 |
| 3 |
又φ(0)=0,结合y=φ(x)的图象(如图),

可知
当m=
| 2 |
| 3 |
当m≤0时,函数g(x)有且只有一个零点.
所以,当m=
| 2 |
| 3 |
看了 设函数f(x)=lnx+mx...的网友还看了以下:
如图所示,用水平力F把一铁块紧压在墙上不动,当F的大小变化时,墙对铁块的压力FN、铁块所受摩擦力F 2020-05-17 …
已知函数f(x)对任意实数a,b有f(a)不等于0,f(a+b)=f(a)f(b),当x小于0时, 2020-05-19 …
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在[0,1]上()A.当f 2020-06-12 …
设f(x)是连续函数,F(x)是f(x)的原函数,则下列结论正确的是?A当f(x)是奇函数时,F( 2020-07-30 …
设是连续函数,是的原函数,则下列结论正确的是:A.当f(x)是奇函数时,F(x)必是偶函数;B当f 2020-08-01 …
设f(x)是连续函数,F(x)是f(x)的原函数,则()A.当f(x)是奇函数时,F(x)必为偶函 2020-08-02 …
为什么机车达到最大速度时a=0,F=f根据P=FV,当P为恒定功率时V和F成反比,那么V不是可以无限 2020-11-24 …
若非零函数f(x)对任意实数a,b均有f(a+b)=f(a)乘f(b),且当x大于零时,f(x)大于 2020-12-07 …
若非零函数f(x)对任意实数a,b均有f(a+b)=f(a)乘f(b),且当x大于零时,f(x)大于 2020-12-07 …
若非零函数f(X)对任意实数a,b,均有f(a+b)+f(a)×f(b)曾黎,且当x<0是,f(X) 2020-12-07 …