如图，椭圆E的方程为x2a2+y2b2=1（a>b>0），点O为坐标原点，点A，B分别是椭圆的右顶点和上顶点，点M在线段AB上，满足BM=2MA，直线OM的斜率为14．（1）求椭圆E的离心率e；（2）设点C的坐标

Question

如图，椭圆E的方程为(x2)/(a2)+(y2)/(b2)=1（a>b>0），点O为坐标原点，点A，B分别是椭圆的右顶点和上顶点，点M在线段AB上，满足BM=2MA，直线OM的斜率为(1)/(4)．

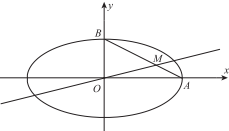
（1）求椭圆E的离心率e；
（2）设点C的坐标为（0，-b），N为线段AC的中点，点N关于直线AB的对称点的纵坐标为(11)/(5)，求椭圆E的方程．

Answer 1

（1）设A（a，0），B（0，b），
∵BM=2MA，由比例性质可得M((2a)/(3)，(b)/(3))，
又∵直线OM的斜率为(1)/(4)，
∴((b)/(3))/((2a)/(3))=(1)/(4)，即(2a)/(3)=(4b)/(3)，
∴a=2b，a²=4b²=4（a²-c²），则e=(c)/(a)=(√(3))/(2)；
（2）∵C（0，-b），A（2b，0），
则由中点坐标公式可得N(b，-(b)/(2))，
直线AB：(x)/(2b)+(y)/(b)=1，即x+2y-2b=0．
设N关于直线AB的对称点是N′(x0，(11)/(5))，
则

(x0+b)/(2)+2×((11)/(5)-(b)/(2))/(2)-2b=0

((11)/(5)-(b)/(2))/(x0-b)=2

，消去x₀得b=2，则a=2b=4．
椭圆方程为：(x2)/(16)+(y2)/(4)=1．