早教吧作业答案频道 -->数学-->
已知一次函数y1=k1x+b与反比例函数y2=k2x相交于点A、B,与y轴交于点C,与x轴交于点D,过点A作AE⊥x轴于点E,点O为DE中点,连接CE,已知S△ADE=4,tan∠DCO=12.(1)求y1和y2的解析式;(2)将△ACE
题目详情
已知一次函数y1=k1x+b与反比例函数y2=
相交于点A、B,与y轴交于点C,与x轴交于点D,过点A作AE⊥x轴于点E,点O为DE中点,连接CE,已知S△ADE=4,tan∠DCO=
.
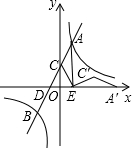
(1)求y1和y2的解析式;
(2)将△ACE绕着点E顺时针旋转90°得△A'C'E,连接AA'、BA',求△AA'B的面积.
| k2 |
| x |
| 1 |
| 2 |

(1)求y1和y2的解析式;
(2)将△ACE绕着点E顺时针旋转90°得△A'C'E,连接AA'、BA',求△AA'B的面积.
▼优质解答
答案和解析
(1)∵O是DE的中点,CO∥AE,
∴CO是△ADE的中位线,
∴AE=2CO,
设CO=m,
∴AE=2m,
∵tan∠DCO=
,
∴
=
,
∴DO=
m,
∴DE=m,
∵S△ADE=4,
∴
DE•AE=4,
∴m2=4,
∴m=2,
∴C(0,2),A(1,4),
将点A(1,4)代入y2=
,
∴k2=4,
将A(1,4)和C(0,2)代入y1=k1x+b,
∴
,
∴解得
,
∴y1=2x+2,y2=
,
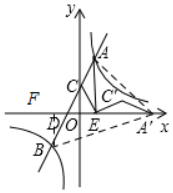
(2)过点B作BF⊥x轴于点F,
联立
,
解得:x=-2或x=1,
∴B(-2,-2),
∴BF=2,
令y=0代入y1=2x+2,
∴D(-1,0),
由题意可知:A′E=AE=4,
∴A′D=OD+OE+AE=6,
∴△AA'B的面积为:
A′D•BF+
A′D•AE=18,
∴CO是△ADE的中位线,
∴AE=2CO,
设CO=m,
∴AE=2m,
∵tan∠DCO=
| 1 |
| 2 |
∴
| DO |
| CO |
| 1 |
| 2 |
∴DO=
| 1 |
| 2 |
∴DE=m,
∵S△ADE=4,
∴
| 1 |
| 2 |
∴m2=4,
∴m=2,
∴C(0,2),A(1,4),
将点A(1,4)代入y2=
| k2 |
| x |
∴k2=4,
将A(1,4)和C(0,2)代入y1=k1x+b,
∴
|
∴解得
|

∴y1=2x+2,y2=
| 4 |
| x |
(2)过点B作BF⊥x轴于点F,
联立
|
解得:x=-2或x=1,
∴B(-2,-2),
∴BF=2,
令y=0代入y1=2x+2,
∴D(-1,0),
由题意可知:A′E=AE=4,
∴A′D=OD+OE+AE=6,
∴△AA'B的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
看了已知一次函数y1=k1x+b与...的网友还看了以下:
(急)已知AD是三角形ABC的中线 BE交AC于点E 交AD于F且AE=EF 求证 AC=BF已知 2020-04-05 …
如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O交AD于E,交BC于F如图,平行四边形 2020-05-15 …
已知矩形ABCD的对角线相交于点O,∠AOD=∠120°,过O作EF⊥BD,交AD于E,交BC于F 2020-05-16 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E交BC于F,边AB折叠后与BC边 2020-05-17 …
如图,⊙O1和⊙O2相交于点A,B.过点A作直线交⊙O1于点C,交⊙O2于点D,M是CD中点,直线 2020-06-03 …
如图,△ABC中,AD平分∠BAC,EF⊥AD交AB于点E,交AC于点F,交BC的延长线于点H.求 2020-06-27 …
已知抛物线y=ax+bx+3与x轴交点于A(1,0)B(-3,0)于y轴交点为C,若点E为第二象限 2020-07-20 …
已知:如图,在三角形ABC中,D、E分别是边AB、AC的中点,AB的垂线过点D交AC于点F,AC的 2020-08-01 …
如图,已知D是∠ABC的平分线与∠ACB的外角平分线的交点,DE平行BC,DE交AB于E,.如图, 2020-08-03 …
如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E, 2020-08-03 …