早教吧作业答案频道 -->数学-->
如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.(1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求CE的长.
题目详情
如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.
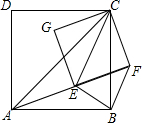
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
▼优质解答
答案和解析
(1)∵四边形ABCD和EFCG均为正方形,
∴
=
=
,
又∵∠ACE+∠BCE=∠BCF+∠BCE=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2):∵△CAE∽△CBF,
∴∠CAE=∠CBF,
=
,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵
=
=
,AE=2
∴
=
,
∴BF=
,
∴EF2=BE2+BF2=3,
∴EF=
,
∵CE2=2EF2=6,
∴CE=
.
∴
| AC |
| BC |
| EC |
| FC |
| 2 |
又∵∠ACE+∠BCE=∠BCF+∠BCE=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2):∵△CAE∽△CBF,
∴∠CAE=∠CBF,
| AE |
| BF |
| AC |
| BC |
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵
| AE |
| BF |
| AC |
| BC |
| 2 |
∴
| 2 |
| BF |
| 2 |
∴BF=
| 2 |
∴EF2=BE2+BF2=3,
∴EF=
| 3 |
∵CE2=2EF2=6,
∴CE=
| 6 |
看了 如图,已知AC、EC分别为四...的网友还看了以下:
已知f(x)=ax^2+bx+1(a,b∈R,a≠0),x∈R时,f(x)min=f(-1)=01 2020-04-26 …
已知函数f(x)=e^x-sinx,证明:f(x)>1在(0,+∞)上恒成立 2020-05-13 …
高中导数问题(2条题)1若函数f(x)=x^3-12x在区间(k-1,k+1)上不是单调函数,则实 2020-05-14 …
f(x)=ax2+bx+c 若a=1,c=0.且|f(x)|≤1在区间(0,1]上恒成立.求b的取 2020-05-14 …
f(x)=x^3+ax^2-a^2x+m(a>0)若对任意的a∈[3,6],不等式f(x)≤1在X 2020-05-16 …
f(x)在[0,1]连续,在(0,1)可导.f(0)=0,f(1)=1.证明存在两点a,b属于(f 2020-06-18 …
定义在R上的偶函数f(x)在(﹣∞,0]上单调递增,若f(a+1)<f(2a-1),求a的取值范围 2020-07-08 …
在f(m,n)中,.m.n.f(m,n)均为非负整数且对任意的m,n有f(0,n)=n+1,f(m 2020-07-31 …
f(x)在[0,1]上二阶可微且f'(0)=f'(1)=0,则存在c,使得f''(c)≥4|f(1) 2020-11-03 …
已知a,b是实数,函数f(x)=x2+ax+1,且y=f(x+1)在定义域上是偶函数,函数g(x)= 2020-12-08 …