早教吧作业答案频道 -->数学-->
已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.(1)求证:BC=CD;(2)若∠A=60°,将线段BC绕着点B逆时针旋转60°,得到线段BE,连接DE,在图中补全图形,并证明四边形BCDE是菱形.
题目详情
已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.
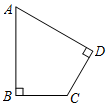
(1)求证:BC=CD;
(2)若∠A=60°,将线段BC绕着点B逆时针旋转60°,得到线段BE,连接DE,在图中补全图形,并证明四边形BCDE是菱形.

(1)求证:BC=CD;
(2)若∠A=60°,将线段BC绕着点B逆时针旋转60°,得到线段BE,连接DE,在图中补全图形,并证明四边形BCDE是菱形.
▼优质解答
答案和解析
(1)连接AC,
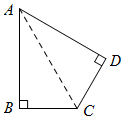
∵∠ABC=∠ADC=90°,
∴△ABC和△ADC均为直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴BC=CD.
(2)补全图如图所示.
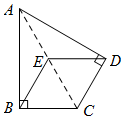
由旋转得BE=BC,∠CBE=60°,
∴BE=CD,
∵∠BAD=60°,∠ABC=∠ADC=90°,
∴∠BCD=120°,
∴∠CBE+∠BCD=180°,
∴BE∥CD,
∴四边形BCDE是平行四边形,
又∵BE=CD,
∴四边形BCDE是菱形.

∵∠ABC=∠ADC=90°,
∴△ABC和△ADC均为直角三角形,
在Rt△ABC和Rt△ADC中,
|
∴Rt△ABC≌Rt△ADC(HL),
∴BC=CD.
(2)补全图如图所示.

由旋转得BE=BC,∠CBE=60°,
∴BE=CD,
∵∠BAD=60°,∠ABC=∠ADC=90°,
∴∠BCD=120°,
∴∠CBE+∠BCD=180°,
∴BE∥CD,
∴四边形BCDE是平行四边形,
又∵BE=CD,
∴四边形BCDE是菱形.
看了 已知:如图,四边形ABCD中...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
知:在平行四边形ABCD中,CD=10,sin角C=4/5,点E、F分别是边AD、对角线BD上的动 2020-05-16 …
如图在正方形ABCD中点E在边AB上再点E作FG垂直于DEFG与边BC相交于点F与边DA的延长线相 2020-06-12 …
线性代数中为何|AA*|=||A|E|?设A为n阶矩阵(n³2),A*为A的伴随阵,证明.证明当R 2020-07-09 …
高中函数题:设f(x)=x/e^x,a≠b,f(a)=f(b),比较a+b与2的大小我是这么想的但 2020-07-13 …
如果矩阵A可逆,证明(A')^-1=(A^-1)'.A’为A的转置矩阵AA^-1=A^-1A=E两 2020-07-20 …
已知向量a≠e,|e|=1,满足:任意t∈R.已知向量a不等于e,|e|=1,对任意t属于R,恒有 2020-07-25 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
矩阵分配律(A-E)(A+E)=(A+E)(A-E),因为两边的乘积都为A^2-E^2,不是在矩阵 2020-07-31 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …