早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:(1)求抛物线的解析式;(2)抛物线的顶点为D,对称轴与x轴交于点E,点A关于DE的对称点为M,连接BM,求BM的长.注:
题目详情
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
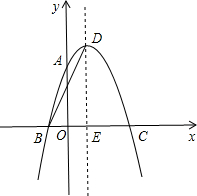
(1)求抛物线的解析式;
(2)抛物线的顶点为D,对称轴与x轴交于点E,点A关于DE的对称点为M,连接BM,求BM的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
,
)

(1)求抛物线的解析式;
(2)抛物线的顶点为D,对称轴与x轴交于点E,点A关于DE的对称点为M,连接BM,求BM的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
▼优质解答
答案和解析
(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),
∴将A(0,3),B(-1,0)代入得:
,
解得:
.
则抛物线解析式为y=-x2+2x+3;
(2) 由顶点坐标(-
由顶点坐标(-
,
)得:D(1,4),
∵抛物线的对称轴与x轴交于点E,
∴OE=1,
∴对称轴为x=1,
∵点A关于DE的对称点为M,
∴M(2,3),
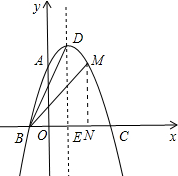
如图所示:过点M作MN⊥x轴于点N,
则N(2,0),
∴BN=3,MN=3,
在Rt△BMN中,根据勾股定理得:BM=
=
=3
.
∴将A(0,3),B(-1,0)代入得:
|
解得:
|
则抛物线解析式为y=-x2+2x+3;
(2)
 由顶点坐标(-
由顶点坐标(-| b |
| 2a |
| 4ac-b2 |
| 2a |
∵抛物线的对称轴与x轴交于点E,
∴OE=1,
∴对称轴为x=1,
∵点A关于DE的对称点为M,
∴M(2,3),
如图所示:过点M作MN⊥x轴于点N,
则N(2,0),
∴BN=3,MN=3,
在Rt△BMN中,根据勾股定理得:BM=
| MN2+BM2 |
| 32+32 |
| 2 |
看了 如图,抛物线y=ax2+2x...的网友还看了以下:
直线y=1/2x+b与曲线y=-1/2x+lnx相切,求b的值直线y=1/2x+b与曲线y=-1/ 2020-04-26 …
计算∫∟(e^y+x)dx+(xe^y-2y)dy,L以点O(0,0)绕曲线y=sinπ/2x到点 2020-05-16 …
已知直线y=-2x+b(b≠0)与x轴交于点A,与y轴交于点B;一抛物线的解析式为y=x2-(b+ 2020-06-14 …
1.已知:直线y=-1/2x-2,若过x轴上一点A(3,0)作与x轴垂直的直线m,求他与直线y=- 2020-06-14 …
已知双曲线y=k/x与直线y=-2x交于A,B两点B点的纵坐标是-4求(1)双曲线的解析式已知双曲 2020-06-21 …
求一下曲线在x=2处的切线方程,超级无敌霹雳啪啦急!1:求一下曲线在x=2处的切线方程f(x)=2 2020-06-21 …
曲线y=x³+2x在点A(1,3)处的切线方程是 2020-06-27 …
求解一道一次函数与二元一次方程组题!马上要!如图,直线y=-2x+b与x轴,y轴分别相交于A,B两 2020-07-18 …
已知直线y=-2x+b(b≠0)与x轴交于点A,与y轴交于点B;一抛物线的解析式为y=x2-(b+1 2020-11-01 …
已知曲线c:y=2x^2,点A(0,-2)及点B(3,a),从点A观察点B要使视线不被圆C挡住求a的 2020-12-05 …