早教吧作业答案频道 -->数学-->
如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.(1)求证:△ABC≌△DEC;(2)求证:DF⊥AB;(3)利用图中阴影部分面积完成勾股定理的
题目详情
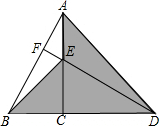
如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:△ABC≌△DEC;
(2)求证:DF⊥AB;
(3)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.

(1)求证:△ABC≌△DEC;
(2)求证:DF⊥AB;
(3)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
▼优质解答
答案和解析
 (1)证明:∵AC⊥BD,∠CAD=45°,
(1)证明:∵AC⊥BD,∠CAD=45°,
∴∠ACD=90°,
∴∠CAD=∠ADC=45°,
∴AC=CD,
在Rt△ABC和Rt△DEC中,
,
∴Rt△ABC≌△Rt△DEC.
(2)∵△ABC≌△DEC,
∴∠BAC=∠EDC,
∵∠EDC+∠CED=90°,∠CED=∠AEF,
∴∠AEF+∠BAC=90°,
∴∠AFE=90°,
∴DF⊥AB.
(2)∵S△BCE+S△ACD=S△ABD-S△ABE,
∴
a2+
b2=
•c•DF-
•c•EF=
•c•(DF-EF)=
•c•DE=
c2,
∴a2+b2=c2
 (1)证明:∵AC⊥BD,∠CAD=45°,
(1)证明:∵AC⊥BD,∠CAD=45°,∴∠ACD=90°,
∴∠CAD=∠ADC=45°,
∴AC=CD,
在Rt△ABC和Rt△DEC中,
|
∴Rt△ABC≌△Rt△DEC.
(2)∵△ABC≌△DEC,
∴∠BAC=∠EDC,
∵∠EDC+∠CED=90°,∠CED=∠AEF,
∴∠AEF+∠BAC=90°,
∴∠AFE=90°,
∴DF⊥AB.
(2)∵S△BCE+S△ACD=S△ABD-S△ABE,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+b2=c2
看了 如图,在△ABD中,AC⊥B...的网友还看了以下:
数学分析习题.设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b)设函数f(x)在[ 2020-07-16 …
f(x)在[0,1]可导,f(x)满足f(0)=0,f(1)=1证明对任意的正数a,b,a/f'( 2020-07-16 …
定积分求证~函数f(x)在[a,b]上连续,且f(x)>0令F(x)=∫(0到x)f(t)dt+∫ 2020-07-31 …
一个导数问题的理解设f(x)在[a,b]上连续,在(a,b)内可导且不恒于常数,f(a)=f(b) 2020-07-31 …
函数f(X)对任意a,b都有f(a+b)=f(a)+f(b)-1,且当X〉0时有f(x)〉1.求证 2020-08-01 …
设g(x)在a,b连续,f(x)在a,b二阶可导,f(a)=g(b)=0,且对任意x属于a,b满足 2020-08-01 …
设映射f:X→Y,A包含于X,B包含于X.证明:f(A∩B)包含于f(A)∩f(B).我的证明是这样 2020-11-01 …
如果函数y=f(x)的图象关于x=a和x=b都对称,证明这个函数满足f[2(a-b)+x]=f(x) 2020-11-19 …
已知b分之a=d分之c=f分之e=...=n分之m,且b+d+f+...+n不等于0,求证b+d+f 2020-12-17 …
1)设f(x)在[a,b]上可微,且f(a)=f(b)=0,证明:在(a,b)内存在一点ξ,使f'( 2020-12-28 …