早教吧作业答案频道 -->数学-->
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:(x2+x+1)0=1(x2+x+1)1=x2+x+1(x2+x+1)2=x4+2x3+3x2+2x+1(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1…观察多项式系数之间的关系,可以仿照杨辉三
题目详情
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
(x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
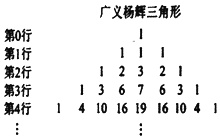
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x8项的系数为67,则实数a值为___.
(x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x8项的系数为67,则实数a值为___.

▼优质解答
答案和解析
由题意可得广义杨辉三角形第5行为1,5,15,30,45,51,45,30,15,5,1,
所以(1+ax)(x2+x+1)5的展开式中,x8项的系数为15+30a=67,
所以a=
.
故答案为:
.
所以(1+ax)(x2+x+1)5的展开式中,x8项的系数为15+30a=67,
所以a=
| 26 |
| 15 |
故答案为:
| 26 |
| 15 |
看了 将三项式(x2+x+1)n展...的网友还看了以下:
设函数f(x)=(1+1/n)的n次方(n∈正整数,n大于1,x∈r)1,对于任意x,证明(f(2 2020-05-14 …
求证数列2,1/2,4/3,.[n+(-1)^(n-1)]/n的极限是1书上给的过程是:|xn-1 2020-05-14 …
求无穷级数∑1/n!的和 2020-05-20 …
无穷级数∑1/n!的和 2020-05-20 …
求1/(n√(n+1))的正项级数用中文说就是1除以(n乘根号下(n+1))的正项级数∞∑1/(n 2020-06-12 …
设y=x^u,求y^n=?这是书上的解法是y'=ux^(u-1),y''=u(u-1)x^(u-2 2020-06-18 …
函数f(x)对任意x∈R都有f(x)+f(1-x)=½(1)求f(½)和f(1/n)+f[(n-1 2020-06-30 …
我们把分数分子是1,分母是正整数的分数叫做分数单位.任何一个单位分数1/n=1/p+1/q(n,p 2020-07-30 …
级数Σ[(-1)^n][n/2^n][(x-1)^2n]当n趋于无穷时lim|Un|^(1/n)= 2020-07-31 …
,,救命···讨论数列Xn=n+(-1)^n-1/n的极限容易看出,当n无限增大时,数列Xn=n+( 2020-11-28 …