早教吧作业答案频道 -->数学-->
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q.(1)证明:Q为BB1的中点;(2)若A1A=4,CD=2,梯形ABCD的面积为6
题目详情
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.
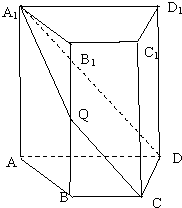
(1)证明:Q为BB1的中点;
(2)若A1A=4,CD=2,梯形 ABCD的面积为6,求平面α与底面ABCD所成角的大小.

(1)证明:Q为BB1的中点;
(2)若A1A=4,CD=2,梯形 ABCD的面积为6,求平面α与底面ABCD所成角的大小.
▼优质解答
答案和解析
(1)证明:∵BQ∥AA1,BC∥AD,
BC∩BQ=B,AD∩AA1=A,
∴平面QBC∥平面A1AD,
从而平面A1CD与这两个平面的交线相互平行,
即QC∥A1D.
故△QBC与△A1AD的对应边相互平行,
于是△QBC∽△A1AD,
∴
=
=
=
,即Q为BB1的中点;
(2) 如图所示,在△ADC中,作AE⊥DC,垂足为E,连接A1E.
又DE⊥AA1,且AA1∩AE=A,
∴DE⊥平面AEA1,∴DE⊥A1E.
∴∠AEA1为平面α与底面ABCD所成二面角的平面角.
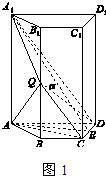
∵BC∥AD,AD=2BC,∴S△ADC=2S△BCA.
又∵梯形ABCD的面积为6,DC=2,
∴S△ADC=4,AE=4.
于是tan∠AEA1=
=1,∠AEA1=
.
故平面α与底面ABCD所成二面角的大小为
.
BC∩BQ=B,AD∩AA1=A,
∴平面QBC∥平面A1AD,
从而平面A1CD与这两个平面的交线相互平行,
即QC∥A1D.
故△QBC与△A1AD的对应边相互平行,
于是△QBC∽△A1AD,
∴
| BQ |
| BB1 |
| BQ |
| AA1 |
| BC |
| AD |
| 1 |
| 2 |
(2) 如图所示,在△ADC中,作AE⊥DC,垂足为E,连接A1E.
又DE⊥AA1,且AA1∩AE=A,
∴DE⊥平面AEA1,∴DE⊥A1E.
∴∠AEA1为平面α与底面ABCD所成二面角的平面角.

∵BC∥AD,AD=2BC,∴S△ADC=2S△BCA.
又∵梯形ABCD的面积为6,DC=2,
∴S△ADC=4,AE=4.
于是tan∠AEA1=
| AA1 |
| AE |
| π |
| 4 |
故平面α与底面ABCD所成二面角的大小为
| π |
| 4 |
看了 如图,四棱柱ABCD-A1B...的网友还看了以下:
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段 2020-06-13 …
(2013•张家界)如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2 2020-06-14 …
元旦捧回家!1、如图1,点C在线段AB上,点M、N分别是线段AB、AC的中点,MN=3cm,AC= 2020-06-25 …
(2014•苏州)如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB 2020-07-01 …
如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转9 2020-07-17 …
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正 2020-07-24 …
如图.AB为O的直径,CD为O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F 2020-07-31 …
(2014•闸北区二模)如图,EF是⊙O的直径,CD交⊙O于M、N,H为MN的中点,EC⊥CD于点C 2020-11-01 …
已知如图,△ABC是等腰三角形,∠ACB=90°,D是斜边AB上的一动点,联结CD,线段CD绕点C逆 2020-12-07 …
一次函数的图像与X轴,Y轴交于AB两点,与反比例函数图像交于CD,且点C纵坐标为1,如果A点坐标为( 2021-01-11 …