早教吧作业答案频道 -->数学-->
如图.AB为O的直径,CD为O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作O的切线,交CD的延长线于H.(1)求证:FH=GH;(2)若AB=2FH=10,tan∠FGH=2,求AG的长.
题目详情
如图.AB为 O的直径,CD为 O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作 O的切线,交CD的延长线于H.
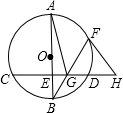
(1)求证:FH=GH;
(2)若AB=2FH=10,tan∠FGH=2,求AG的长.

(1)求证:FH=GH;
(2)若AB=2FH=10,tan∠FGH=2,求AG的长.
▼优质解答
答案和解析
(1)证明:连接OF,如图1所示.
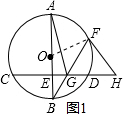
∵HF与 O相切于点F,
∴∠OFH=90°,
∴∠GFH=90°-∠OFB.
∵OB=OF,
∴∠OFB=∠OBF.
∵AB⊥CD于E,
∴∠BEG=90°,
∴∠BGE=180°-∠BEG-∠EBG=90°-∠OBF.
∵OB=OF,
∴∠OBF=∠OFB,
∴∠GFH=∠BGE,
又∵∠BGE=∠FGH,
∴∠GFH=∠FGH,
∴FH=GH.
(2) 过H作HM⊥GF于点M,连接AF,如图2所示.
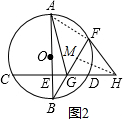
∵AB=2FH=10,tan∠FGH=2,
∴设GM=a,AF=b,
则HM=GF=2a,BF=2b,
由勾股定理得:GH=
=
a=5,AB=
=
b=10,
∴a=
,b=2
.
BG=BF-GF=2b-2a=2
,
∵tan∠BGE=2,
∴cos∠BGE=
,
∴EG=BG•cos∠BGE=2,BG=EG•tan∠BGE=4.
在Rt△AEG中,AE=AB-BE=6,EG=2,
∴AG=
=2
.

∵HF与 O相切于点F,
∴∠OFH=90°,
∴∠GFH=90°-∠OFB.
∵OB=OF,
∴∠OFB=∠OBF.
∵AB⊥CD于E,
∴∠BEG=90°,
∴∠BGE=180°-∠BEG-∠EBG=90°-∠OBF.
∵OB=OF,
∴∠OBF=∠OFB,
∴∠GFH=∠BGE,
又∵∠BGE=∠FGH,
∴∠GFH=∠FGH,
∴FH=GH.
(2) 过H作HM⊥GF于点M,连接AF,如图2所示.

∵AB=2FH=10,tan∠FGH=2,
∴设GM=a,AF=b,
则HM=GF=2a,BF=2b,
由勾股定理得:GH=
| GM2+HM2 |
| 5 |
| AF2+BF2 |
| 5 |
∴a=
| 5 |
| 5 |
BG=BF-GF=2b-2a=2
| 5 |
∵tan∠BGE=2,
∴cos∠BGE=
| ||
| 5 |
∴EG=BG•cos∠BGE=2,BG=EG•tan∠BGE=4.
在Rt△AEG中,AE=AB-BE=6,EG=2,
∴AG=
| AE2+EG2 |
| 10 |
看了 如图.AB为O的直径,CD为...的网友还看了以下:
如图,EF分别为正方形ABCD的边AB,AD的中点,DE,CF相交于点P,DE的延长线交CB的延长 2020-05-16 …
BE是圆O的直径,AC.BC相交于点C,AC,BC与圆O分别相切于点D,B,AC,BC交圆O于点D 2020-06-03 …
已知:如图,Rt△ABC中,点D在斜边AB上,以AD为直径的⊙O与BC相切于点E,连接DE并延长, 2020-06-03 …
如图所示,四边形ABCD内接于圆O,AD是圆O的直径,AD=4,AB=BC=1,延长DC,AB交于 2020-06-05 …
如图所示,四边形ABCD为平行四边形,AD=a,BE//AC,DE交AC的延长线于点F,交BE于点 2020-06-06 …
已知:如图,在梯形abcd中,ad//bc,角cab=90度,ab=bc=8,点e在边ab上,de 2020-06-12 …
如图,在圆O中AB是直径,AT是经过点A的切线,弦CD垂直AB于P点,线段CP的中点为Q,连接BQ 2020-06-12 …
如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF, 2020-06-13 …
(2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连 2020-06-23 …
已知a,b分别是等腰三角形的一腰和底边的长,求证:关于x的二元三项式x的平方-4ax+b的平方一定 2020-07-07 …