早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转90°得到线段CE,连接DE,AE,BD.(1)依题意补全图1;(2)判断AE与BD的数量关系与位置关系并加以证明;(3)若0°<
题目详情
如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转90°得到线段CE,连接DE,AE,BD.
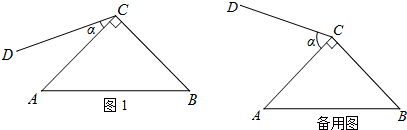
(1)依题意补全图1;
(2)判断AE与BD的数量关系与位置关系并加以证明;
(3)若0°<α≤64°,AB=4,AE与BD相交于点G,求点G到直线AB的距离的最大值.请写出求解的思路(可以不写出计算结果).

(1)依题意补全图1;
(2)判断AE与BD的数量关系与位置关系并加以证明;
(3)若0°<α≤64°,AB=4,AE与BD相交于点G,求点G到直线AB的距离的最大值.请写出求解的思路(可以不写出计算结果).
▼优质解答
答案和解析
(1)补全图形,如图1所示.
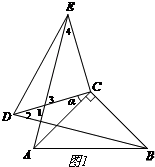
(2)AE与BD的数量关系:AE=BD,
AE与BD的位置关系:AE⊥BD.
证明:∵∠ACB=∠DCE=90°,
∴∠ACB+α=∠DCE+α.
即∠BCD=∠ACE.
∵BC=AC,CD=BC,
∴△BCD≌△ACE.
∴AE=BD.
∴∠4=∠CBD.
∵∠CBD=∠2,
∴∠2=∠4.
∵∠3+∠4=90°,∠1=∠3,
∴∠1+∠2=90°.
即AE⊥BD.
(3)如图2,
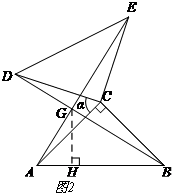
过点G作GH⊥AB于H.
由线段CD的运动可知,当α=64°时GH的长度最大.
∵CB=CD,
∴∠CBD=∠CDB,
∴∠CBD=
=13°,
∴∠DBA=32°.
由(2)可知,∠AGB=90°,
∴∠GAB=58°,
在Rt△GAH中,tan∠GAB=tan58°=
,
∴AH=
,
和Rt△GBH中,tan∠DBA=tan32°=
,
∴BH=
,
∵AB=4,
∴AH+BH=4,
∴
+
=3,
∴GH=3(tan58°+tan32°).

(2)AE与BD的数量关系:AE=BD,
AE与BD的位置关系:AE⊥BD.
证明:∵∠ACB=∠DCE=90°,
∴∠ACB+α=∠DCE+α.
即∠BCD=∠ACE.
∵BC=AC,CD=BC,
∴△BCD≌△ACE.
∴AE=BD.
∴∠4=∠CBD.
∵∠CBD=∠2,
∴∠2=∠4.
∵∠3+∠4=90°,∠1=∠3,
∴∠1+∠2=90°.
即AE⊥BD.
(3)如图2,

过点G作GH⊥AB于H.
由线段CD的运动可知,当α=64°时GH的长度最大.
∵CB=CD,
∴∠CBD=∠CDB,
∴∠CBD=
| 180°-90°-64° |
| 2 |
∴∠DBA=32°.
由(2)可知,∠AGB=90°,
∴∠GAB=58°,
在Rt△GAH中,tan∠GAB=tan58°=
| GH |
| AH |
∴AH=
| GH |
| tan58° |
和Rt△GBH中,tan∠DBA=tan32°=
| GH |
| BH |
∴BH=
| GH |
| tan32° |
∵AB=4,
∴AH+BH=4,
∴
| GH |
| tan58° |
| GH |
| tan32° |
∴GH=3(tan58°+tan32°).
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
在平面直角坐标系中,如图1,将线段ab平移至线段cd,连接c,d坐标(1)诺A(-1,0)、B(0 2020-05-15 …
根据每个细胞中DNA的相对含量不同,将某种连续增殖的动物细胞归为甲、乙、丙三组,每组细胞数如下图1 2020-05-17 …
下列与细胞分裂相关的坐标图中(不考虑细胞质DNA),有关叙述正确的是()A.图甲中BC段细胞的名称 2020-05-23 …
如图在rt三角形abc中角acb等于九十度点df分别在abac上cf等于cb连接CD,将线段c绕点 2020-07-18 …
如图所示的某段电路中,A、B、C、D、E是四个接线柱.A接电源的负极,E接电源的正极.(1)用导线 2020-07-29 …
如图,在4×6的正方形网格,点A、B、C、D、E、F都在格点上,连接C、D、E、F中任意两点得到的 2020-08-02 …
如图,在4×6的正方形网格,点A、B、C、D、E、F都在格点上,连接C、D、E、F中任意两点得到的 2020-08-02 …
如图,一根细长的绳子,沿中间对折,再沿对折后的中间对折,这样连续沿中间对折4次,用剪刀沿4次对折后的 2020-11-07 …
如图是植物细胞有丝分裂过程中不同时期染色体和DNA变化曲线图及细胞分裂图象,下列相关叙述中正确的是( 2020-11-30 …
图中a→d表示连续分裂的动物细胞的两个细胞周期.下列叙述中不正确的是()A.a过程完成中心体的复制B 2021-01-14 …