在直角坐标系中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为，曲线C2的直角坐标方程为．（1）求曲线C1的直角坐标方程；（2）已知为曲线C2上一点，

Question

在直角坐标系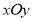 中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1

的极坐标方程为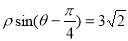 ，曲线C2的直角坐标方程为 ．

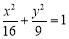（1）求曲线C1的直角坐标方程；

（2）已知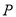 为曲线C2上一点，Q为曲线C1上一点，求P、Q两点间距离的最小值．

 

Answer 1

（1）；（2）

分 析：
（1）将参数方程转化为直角坐标系下的普通方程，需要根据参数方程的结构特征，选取恰当的消参方法，常见的消参方法有：代入消参法、加减消参法、平方消参法；（2）将参数方程转化为普通方程时，要注意两种方程的等价性，不要增解、漏解，若有范围限制，要标出的取值范围；（3）先转化为普通方程和直角坐标方程后根据题意设点根据点到直线的距离公式.试题
解析：

（1）由得， 3分即 所以直线l的直角坐标方程为； 6分（2）P为上一点，设，其中 8分则P到直线l的距离 其中 所以当时 的最大值为．
考点：
（1）参数方程与普通方程的互化；（2）参数方程的应用.