早教吧作业答案频道 -->数学-->
已知双曲线C的渐近线方程为y=±x,一个焦点为(22,0).(1)求双曲线C的方程;(2)过双曲线C上的任意一点P,分别作这两条渐近线的平行线与这两条渐近线得到四边形ODPG,证明四边形ODPG
题目详情
已知双曲线C的渐近线方程为y=±x,一个焦点为(2
,0).
(1)求双曲线C的方程;
(2)过双曲线C上的任意一点P,分别作这两条渐近线的平行线与这两条渐近线得到四边形ODPG,证明四边形ODPG的面积是一个定值;
(3)(普通中学做)命题甲:设直线x=0与y=h(h>0)在第一象限内与渐近线y=x所围成的三角形OMN绕着y轴旋转一周所得几何体的体积.
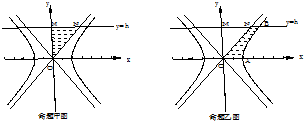
(重点中学做)命题乙:设直线y=0与y=h(h>0)在第一象限内与双曲线及渐近线所围成的如图所示的图形OABN,求它绕y轴旋转一圈所得几何体的体积.
| 2 |
(1)求双曲线C的方程;
(2)过双曲线C上的任意一点P,分别作这两条渐近线的平行线与这两条渐近线得到四边形ODPG,证明四边形ODPG的面积是一个定值;
(3)(普通中学做)命题甲:设直线x=0与y=h(h>0)在第一象限内与渐近线y=x所围成的三角形OMN绕着y轴旋转一周所得几何体的体积.

(重点中学做)命题乙:设直线y=0与y=h(h>0)在第一象限内与双曲线及渐近线所围成的如图所示的图形OABN,求它绕y轴旋转一圈所得几何体的体积.
▼优质解答
答案和解析
(1)设双曲线方程为
-
=1(a>0,b>0),
∵c=2
,渐近线方程为y=±x,
∴a2+b2=8,且a=b,从而a=b=2,双曲线C的方程为
-
=1.…(4分)
(2)由于两条渐近线互相垂直,∴四边形ODPG为矩形.
设P(x0,y0),则
-
=1,
∵|PD|•|PG|=
•
=
=2.
∴四边形ODPG的面积是一个定值.…(8分)
(3)命题甲:设y=h在第一象限内与渐近线的交点N的横坐标x=h,三角形OMN绕着y轴旋转一周所得几何体是一个以|MN|为半径,OM为高的圆锥,
体积等于
(立方单位)…(12分)
命题乙:设y=h在第一象限内与渐近线的交点N的横坐标x=h,与双曲线第一象限的交点B的横坐标x=
,
记y=h与y轴交于点M,因为π|MB|2-π|MN|2=4π
根据祖暅原理,可得旋转体的体积为4πh(立方单位)…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
∵c=2
| 2 |
∴a2+b2=8,且a=b,从而a=b=2,双曲线C的方程为
| x2 |
| 4 |
| y2 |
| 4 |
(2)由于两条渐近线互相垂直,∴四边形ODPG为矩形.
设P(x0,y0),则
| ||
| 4 |
| ||
| 4 |
∵|PD|•|PG|=
| |x0-y0| | ||
|
| |x0+y0| | ||
|
|
| ||||
| 2 |
∴四边形ODPG的面积是一个定值.…(8分)
(3)命题甲:设y=h在第一象限内与渐近线的交点N的横坐标x=h,三角形OMN绕着y轴旋转一周所得几何体是一个以|MN|为半径,OM为高的圆锥,
体积等于
| πh3 |
| 3 |
命题乙:设y=h在第一象限内与渐近线的交点N的横坐标x=h,与双曲线第一象限的交点B的横坐标x=
| 4+h2 |
记y=h与y轴交于点M,因为π|MB|2-π|MN|2=4π
根据祖暅原理,可得旋转体的体积为4πh(立方单位)…(12分)
看了 已知双曲线C的渐近线方程为y...的网友还看了以下:
已知下面的哪些数据,可以计算出地球的质量M(G已知)()A.人造地球卫星在地面附近绕行时的速度和运 2020-04-09 …
已知平行四边形ABCD的周长是44厘米.AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的 2020-06-07 …
找行近字在组词.1,盲()行近字是()().2,滔()行近字是()()3,扣()行近找行近字在组词 2020-06-30 …
在word中每页22行每行28字怎么排我在文档网格中已经设置了每行28个字,每页22行,行数到是对 2020-07-17 …
截至2012年8月17日,我国内地已有22家中小企业在深圳证券交易所通过了备案,其中有15家已经完成 2020-11-11 …
易语言修改文本中间的一段字例如D:\1\1.TXT的内容为:1+1=22+2=4……4=4=88+8 2020-11-28 …
一艘宇宙飞船飞近某一新发现的行星,并进入靠近该行星表面的圆形轨道绕行数圈后,着陆在该行星上.飞船上备 2020-11-28 …
课题关爱我们的眼睛内容近视眼在我国已经到了接近流行的程度,许多大城市的重点学校学生近视率:小学生近1 2020-11-28 …
近地卫星在100-200km的高度飞行,与地球半径6400km相比,完全可以说是在“地面附近”飞行. 2020-12-15 …
有一空间探测器围绕一球状行星作圆周运动.已知该行星的半径r=1750km,探测器在靠近行星表面附近运 2021-02-02 …