早教吧作业答案频道 -->数学-->
如图,AB为圆O的直径,P是AB延长线上一点,割线PCD交圆O于C,D两点,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.(1)证明:F、E、C、D四点共圆;(2)若AP=10,BP=2,CP=3,求sin∠DPF的
题目详情
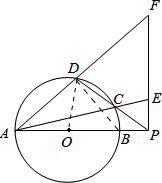
如图,AB为圆O的直径,P是AB延长线上一点,割线PCD交圆O于C,D两点,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.

(1)证明:F、E、C、D四点共圆;
(2)若AP=10,BP=2,CP=3,求sin∠DPF的值.

(1)证明:F、E、C、D四点共圆;
(2)若AP=10,BP=2,CP=3,求sin∠DPF的值.
▼优质解答
答案和解析
 (1)证明:连接BD,
(1)证明:连接BD,
由AB为直径,可得∠ADB=90°,
由∠APF=∠ADB=90°,
且∠DAB=∠PAF,
可得△ADB∽△APF,
即有∠ABD=∠AFP,
又∠ACD=∠ABD,
可得∠ACD=∠AFP,
即∠DCE+∠DFE=180°,
可得F、E、C、D四点共圆;
(2)AP=10,BP=2,CP=3,
由圆的割线定理可得,PB•PA=PC•PD,
即为2×10=3PD,
即PD=
.
PA=PB+AB,即AB=PA-PB=10-2=8.
可得OD=4,
连接OD,在△POD中,PO=6,PD=
,OD=4,
由余弦定理可得cos∠DPO=
=
=
.
则sin∠DPF=sin(90°-∠DPO)=cos∠DPO=
.
 (1)证明:连接BD,
(1)证明:连接BD,由AB为直径,可得∠ADB=90°,
由∠APF=∠ADB=90°,
且∠DAB=∠PAF,
可得△ADB∽△APF,
即有∠ABD=∠AFP,
又∠ACD=∠ABD,
可得∠ACD=∠AFP,
即∠DCE+∠DFE=180°,
可得F、E、C、D四点共圆;
(2)AP=10,BP=2,CP=3,
由圆的割线定理可得,PB•PA=PC•PD,
即为2×10=3PD,
即PD=
| 20 |
| 3 |
PA=PB+AB,即AB=PA-PB=10-2=8.
可得OD=4,
连接OD,在△POD中,PO=6,PD=
| 20 |
| 3 |
由余弦定理可得cos∠DPO=
| PD2+PO2-OD2 |
| 2PD•PO |
=
| ||
2×
|
| 29 |
| 36 |
则sin∠DPF=sin(90°-∠DPO)=cos∠DPO=
| 29 |
| 36 |
看了 如图,AB为圆O的直径,P是...的网友还看了以下:
某校四年级学生参加割草活动,四1班割草25.6千克,四2班、四3千克分别割草27.7千克和24.5 2020-05-14 …
1.一个圆柱形钢材,沿底面直径割开成两个相等的半圆柱体,如果已知一个割面的面积是960平方厘米,半 2020-06-03 …
把一个平行四边形割补成长方形,割补后的长方形与原来的平行四边形比较()A.周长变,面积不变B.周长 2020-06-22 …
某农场有198公顷的水稻田,前四天收割了72公顷,照这样计算,剩下的还要多少天才能收割完?(用比例 2020-07-18 …
在曲线y=e^x上取两点P(0,1)和Q(1,e),作割线PQ.问在该曲线上哪一点处曲线的切线平 2020-07-31 …
AB为圆O的直径,割线L交圆o于M、N,AB垂直于L,并且交圆O于E,BD垂直于L于D,若AB=1 2020-07-31 …
AB是圆O的直径,割线L交圆O于点M和N,AC⊥L,且交圆O于点E,BD⊥L,点CD是垂足(1)O 2020-07-31 …
“苍天苍天泪如雨,倭人竟割台湾去。”台湾同胞怀着悲愤的心情奔走相告,“哭声达于四野”。“割台湾”是近 2020-11-25 …
著名的科学家诺贝尔经过长期的试验,研制出安全炸药.炸药三硝酸甘油酯(C3四e她3O4)发生爆炸的化学 2020-12-22 …
推导平行四边形面积公式:把一个平行四边形割补法,转成换成一个长方形,这个平行四边形的面积与原来平行 2021-01-07 …