早教吧作业答案频道 -->数学-->
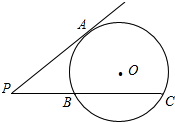
如图所示,O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是O外一点,过点P作O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与O的交点.若PA,PB,PC的长都
题目详情
如图所示, O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是 O外一点,过点P作 O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与 O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.

▼优质解答
答案和解析
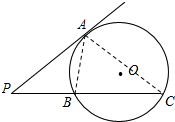 设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
由题设及①知,x1,x2都是整数.从①,②消去k,得2x1x2+x1+x2=4,(2x1+1)(2x2+1)=9.
由上式知,x2≤4,且当k=0时,x2=4,故最大的整数根为4.
于是 O的直径为4,所以BC≤4.
因为BC=PC-PB为正整数,所以BC=1,2,3或4.
连接AB,AC,因为∠PAB=∠PCA,所以△PAB∽△PCA,
=
.
故PA2=PB(PB+BC)③
(1)当BC=1时,由③得,PA2=PB2+PB,于是PB2<PA2<(PB+1)2,矛盾!
(2)当BC=2时,由③得,PA2=PB2+2PB,于是PB2<PA2<(PB+1)2,矛盾!
(3)当BC=3时,由③得,PA2=PB2+3PB,于是(PA-PB)(PA+PB)=3PB,
由于PB不是合数,结合PA-PB<PA+PB,
故只可能
,
,
,
解得PA=2,PB=1.
此时PA2+PB2+PC2=21.
(4)当BC=4,由③得,PA2=PB2+4PB,于是(PB+1)2<PB2+4PB=PA2<(PB+2)2,矛盾.
综上所述PA2+PB2+PC2=21.
 设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②由题设及①知,x1,x2都是整数.从①,②消去k,得2x1x2+x1+x2=4,(2x1+1)(2x2+1)=9.
由上式知,x2≤4,且当k=0时,x2=4,故最大的整数根为4.
于是 O的直径为4,所以BC≤4.
因为BC=PC-PB为正整数,所以BC=1,2,3或4.
连接AB,AC,因为∠PAB=∠PCA,所以△PAB∽△PCA,
| PA |
| PB |
| PC |
| PA |
故PA2=PB(PB+BC)③
(1)当BC=1时,由③得,PA2=PB2+PB,于是PB2<PA2<(PB+1)2,矛盾!
(2)当BC=2时,由③得,PA2=PB2+2PB,于是PB2<PA2<(PB+1)2,矛盾!
(3)当BC=3时,由③得,PA2=PB2+3PB,于是(PA-PB)(PA+PB)=3PB,
由于PB不是合数,结合PA-PB<PA+PB,
故只可能
|
|
|
解得PA=2,PB=1.
此时PA2+PB2+PC2=21.
(4)当BC=4,由③得,PA2=PB2+4PB,于是(PB+1)2<PB2+4PB=PA2<(PB+2)2,矛盾.
综上所述PA2+PB2+PC2=21.
看了 如图所示,O的直径的长是关于...的网友还看了以下:
13,解方程:3^x+4^x+5^x=6^x,请帮忙分析我的疑惑问题,两边除以6^x(1/2)^x 2020-05-17 …
设x,y都是有理数,且满足方程(1/2+π/3)x+(1/3+π/2)y-4-π=o,求x,y的值 2020-06-14 …
1.R上定义运算@:x@y=x(1-y),若不等式(x-a)@(x+a)<1对任何实数x都成立那么 2020-08-01 …
不等式的证明1.已知x,y属于R.x^2+y^2≤1,求证绝对值(x^2+2xy-y^2)≤根号2 2020-08-03 …
就是一直算下去一个公式2+2+X=3X然后每次都把X加下去后面再增加一个数例如2+2+X+Y=3Y2 2020-10-31 …
如果具有下述性质的x都是**M中的元素,即x=a+√2b,且a,b∈,则下列元素中不属于**M的元素 2020-11-26 …
1、设函数f(x)为奇函数,且对任意x,y属于R都有f(x)-f(y)=f(x-y),当x0,f(1 2020-12-08 …
求二次函数未知数的取值范围已知二次函数f(x)=ax^2+bx+c满足:对任意实数x都有f(x)≥x 2020-12-08 …
已知二次函数f(x)的二次项系数为负数,对于任意实数x,都有f(2-x)=f(2+x),试问在f(1 2021-01-11 …
初1分式加减(都是教育学里的题目)1.a-a^2/a-1+12.(x+2/x^2-2x-x-1/x^ 2021-01-23 …