早教吧作业答案频道 -->数学-->
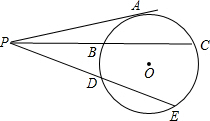
如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.(1)求证:PA2=PB?PC;(2)割线PEF交⊙O于点E、F,且PB=BC=4,PE=6,求EF的长.
题目详情
 如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.
如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.(1)求证:PA 2 =PB?PC;
(2)割线PEF交⊙O于点E、F,且PB=BC=4,PE=6,求EF的长.
▼优质解答
答案和解析
(1)连接AB、AC、BO、AO,∵PA切⊙O于点A,∴PA⊥AO,即∠PAB+∠BAO=90°,又∵2∠BAO+∠O=180°,∴∠PAB=∠O,∵∠C=∠O,∴∠PAB=∠C,∴△PAB∽△PCA,∴,即PA2=PB?PC.(2)∵PA2=PB?PC,同理,PA2=PD?PE,∴PD?PE=PB?PC,且PB=BC=4,PE=6,∴,即DE=PE-PD=6-=.
分析:
(1)连接AB、AC、BO、AO,可证得△PAB∽△PCA,则,即PA2=PB?PC(2)由PA2=PB?PC,同理得,PA2=PD?PE,可证得PD?PE=PB?PC,根据题意可求得PD,即得出DE的长.
点评:
本题考查的是切割线定理,相似三角形的判定和性质,是基础知识要熟练掌握.
分析:
(1)连接AB、AC、BO、AO,可证得△PAB∽△PCA,则,即PA2=PB?PC(2)由PA2=PB?PC,同理得,PA2=PD?PE,可证得PD?PE=PB?PC,根据题意可求得PD,即得出DE的长.
点评:
本题考查的是切割线定理,相似三角形的判定和性质,是基础知识要熟练掌握.
看了 如图,PA切⊙O于点A,割线...的网友还看了以下:
命题:“当abc=0时,a=0或b=0或c=0”的逆否命题为()A.若a=0或b=0或c=0,则a 2020-08-02 …
a、b是异面直线,正确的有哪些?为什么.A.有且只有一个平面同时平行于直线a、b?B.有且只有一个 2020-08-02 …
平面直角坐标系xoy中,已知A(-1,0),B(0,1),求满足PA2-PB2=4且在x²+y²= 2020-08-03 …
已知f(x)=x^2-x+k,且log2f(a)=2,f(log2a)=k,a>0且a≠1已知f(x 2020-11-01 …
在空间直角坐标系中,若向量a→=(−2,1,3),b→=(1,−1,1),c→=(1,−12,−32 2020-11-02 …
已知两条直线a、b及平面α有四个命题:①若a∥b且a∥α则b∥α;②若a⊥α且b⊥α则a∥b;③若a 2020-11-02 …
已知直线a和平面α,则能推出a∥α的是()A.存在一条直线b,a∥b,且b∥αB.存在一条直线b,a 2020-11-02 …
如图所示表示A、B、C三种物质的质量跟体积的关系,由图可知()A.ρA>ρB>ρC,且ρA>ρ水B. 2020-11-03 …
这里有字数限制,所以写在下面了当A<500,且A*B<20,则C=20,否则C=A*B;当A<200 2020-12-22 …
已知直线a,b和平面α,下列推理错误的是()A.a⊥α且b⊂α⇒a⊥bB.a∥b且a⊥α⇒b⊥αC. 2020-12-23 …