已知动圆P过定点A（-3，0），并且与定圆B：（x-3）2+y2=64内切．（1）求动圆圆心P的轨迹E的方程；（2）过M（2，1）作直线l交E于A，B两点，且M恰是AB中点，求直线l的方程．

Question

已知动圆P过定点A（-3，0），并且与定圆B：（x-3）²+y²=64内切．
（1）求动圆圆心P的轨迹E的方程；
（2）过M（2，1）作直线l交E于A，B两点，且M恰是AB中点，求直线l的方程．

Answer 1

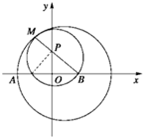（1）如图，设动圆P和定圆B内切于M，则动圆的圆心P到两点，即定点A（-3，0）和定圆的圆心B（3，0）的距离之和恰好等于定圆半径，
即|PA|+|PB|=|PM|+|PB|=|BM|=8．
∴点P的轨迹是以A、B为焦点的椭圆，a=4，c=3，b=√(7)，
∴动圆圆心P的轨迹E的方程为(x2)/(16)+(y2)/(7)=1；
（2）设A（x₁，y₁）、B（x₂，y₂），则x₁+x₂=4，y₁+y₂=2，
代入椭圆方程，作差整理可得k_AB=-(7)/(8)，
又∴直线l的方程为y-1=-(7)/(8)（x-2），
即7x+8y-22=0．