早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.(1)求证:AD平分∠BAC;(2)若⊙O的直径为10,sin∠DAC=55,求BD的长.
题目详情
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
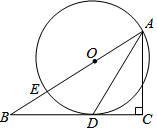
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=
,求BD的长.

(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=
| ||
| 5 |
▼优质解答
答案和解析
(1)连接OD.
∵OD、OA是⊙O的半径,
∴OA=OD.
∴∠OAD=∠ODA.
∵点D是⊙O的切点,
∴∠ODC=90°
又∵∠C=90°,
∴OD∥AC.
∴∠ODA=∠DAC,
∴∠OAD=∠CAD,
∴AD平分∠BAC.
(2)如图2所示:连接ED.
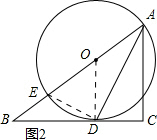
∵⊙O的半径为5,AE是圆O的直径,
∴AE=10,∠EDA=90°.
∵∠EAD=∠CAD,sin∠DAC=
,
∴AD=
×10=4
.
∴DC=
×4
=4,AC=
×4
=8.
∵OD∥AC,
∴△BOD∽△BAC,
∴
=
,即
=
,
解得:BD=
.
∵OD、OA是⊙O的半径,
∴OA=OD.
∴∠OAD=∠ODA.
∵点D是⊙O的切点,
∴∠ODC=90°
又∵∠C=90°,
∴OD∥AC.
∴∠ODA=∠DAC,
∴∠OAD=∠CAD,
∴AD平分∠BAC.
(2)如图2所示:连接ED.

∵⊙O的半径为5,AE是圆O的直径,
∴AE=10,∠EDA=90°.
∵∠EAD=∠CAD,sin∠DAC=
| ||
| 5 |
∴AD=
2
| ||
| 5 |
| 5 |
∴DC=
| ||
| 5 |
| 5 |
2
| ||
| 5 |
| 5 |
∵OD∥AC,
∴△BOD∽△BAC,
∴
| OD |
| AC |
| BD |
| BC |
| 5 |
| 8 |
| BD |
| BD+4 |
解得:BD=
| 20 |
| 3 |
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
数集A满足条件若a∈A则有(1+a)/(1-a)∈A(a≠1)数集A满足条件若a∈A则有(1+a) 2020-04-05 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
求4道题目,50分1.已知a+b=10,求a的平方+b的平方的最小值2.已知(2x-3)(x^2+ 2020-04-11 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
已知函数f(x)=ex+ax-a(a∈R且a≠0).(Ⅰ)若函数f(x)在x=0处取得极值,求实数 2020-07-21 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
商品A是商品B的替代品,商品B与商品C是互补品的关系,当商品B价格上升时,商品A与C的需求会发生的变 2020-12-01 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …